题目内容
（2013•韶关二模）4件A商品与5件B商品的价格之和不小于20元，而6件A商 品与3件B商品的价格之和不大于24元，则买3件A商品与9件B商品至少需要（ ）
分析：设一件A、B商品的价格分别为x元、y元，则购买3件A商品与9件B商品共需要z=3x+9y元．给出满足条件的不等式组，并作出不等式组表示的平面区域，得如图的△ABC及其内部，再将目标函数对应的直线进行平移，可得当x=
且y=
时，z取得最小值．
| 10 |
| 3 |
| 4 |
| 3 |
解答：解：设一件A商品的价格为x元，一件B商品的价格为y元，买3件A商品与9件B商品需要z元，则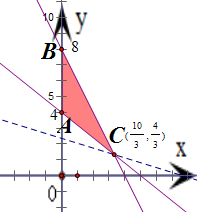
z=3x+9y，其中x、y满足不等式
作出不等式组表示的平面区域，
得到如图的△ABC及其内部，其中A（0，4），B（0，8），C（
，
）
设z=F（x，y）=3x+9y，将直线l：z=3x+9y进行平移，
当l经过点C时，目标函数z达到最小值，
∴z最小值=F（
，
）=3×
+9×
=22
因此，当一件A商品的价格为
元，一件B商品的价格为
元时，
可使则买3件A商品与9件B商品费用最小，最小费用为22元
故选：B
z=3x+9y，其中x、y满足不等式
|
作出不等式组表示的平面区域，
得到如图的△ABC及其内部，其中A（0，4），B（0，8），C（
| 10 |
| 3 |
| 4 |
| 3 |
设z=F（x，y）=3x+9y，将直线l：z=3x+9y进行平移，
当l经过点C时，目标函数z达到最小值，
∴z最小值=F（
| 10 |
| 3 |
| 4 |
| 3 |
| 10 |
| 3 |
| 4 |
| 3 |
因此，当一件A商品的价格为
| 10 |
| 3 |
| 4 |
| 3 |
可使则买3件A商品与9件B商品费用最小，最小费用为22元
故选：B
点评：本题给出实际应用问题，求目标函数z=3x+9y的最小值，着重考查了二元一次不等式组表示的平面区域和简单的线性规划的应用等知识，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目