题目内容
19.已知函数f(x)=$\frac{1}{{4}^{x}-1}$-a是奇函数.(1)求函数f(x)的解析式并写出它的单调区间(不要求证明);
(2)设x1>0,x2>0,x1≠x2,判断$\frac{f({x}_{1})+f({x}_{2})}{2}$与f($\frac{{x}_{1}+{x}_{2}}{2}$)的大小,并给出证明.
分析 (1)根据奇函数的定义,求f(-x)=-f(x),经过通分整理便可得到(2a+1)•4x-(2a+1)=0,这个等式对于定义域内任意x都成立,只能2a+1=0,求出a,便可得到f(x)的解析式.求f′(x),根据其符号,便可找出f(x)定义域内包含的单调区间;
(2)作差比较$\frac{f({x}_{1})+f({x}_{2})}{2}$与f($\frac{{x}_{1}+{x}_{2}}{2}$)的大小:$\frac{f({x}_{1})+f({x}_{2})}{2}$-f($\frac{{x}_{1}+{x}_{2}}{2}$)=$\frac{1}{2}[(\frac{1}{{4}^{{x}_{1}}-1}-\frac{1}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1})+(\frac{1}{{4}^{{x}_{2}}-1}-\frac{1}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1})]$,接下去进行通分并提取公因式即可判断$\frac{f({x}_{1})+f({x}_{2})}{2}$-f($\frac{{x}_{1}+{x}_{2}}{2}$)的符号,从而判断出大小关系.
解答 解:(1)f(x)是奇函数;
∴$f(-x)=\frac{1}{{4}^{-x}-1}-a=\frac{{4}^{x}-a+a•{4}^{x}}{1-{4}^{x}}$=$-(\frac{1}{{4}^{x}-1}-a)=-\frac{1-a•{4}^{x}+a}{{4}^{x}-1}$;
∴4x-a+a•4x=1-a•4x+a;
∴(2a+1)•4x-(2a+1)=0;
∴2a+1=0,$a=-\frac{1}{2}$;
∴$f(x)=\frac{1}{{4}^{x}-1}+\frac{1}{2}$,$f′(x)=\frac{2ln2•{4}^{x}}{({4}^{x}-1)^{2}}>0$;
∴f(x)在(-∞,0),(0,+∞)上单调递增;
即f(x)的单调增区间为(-∞,0),(0,+∞);
(2)$\frac{f({x}_{1})+f({x}_{2})}{2}-f(\frac{{x}_{1}+{x}_{2}}{2})$=$\frac{1}{2}(\frac{1}{{4}^{{x}_{1}}-1}+\frac{1}{{4}^{{x}_{2}}-1})$$-\frac{1}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1}$
=$\frac{1}{2}[(\frac{1}{{4}^{{x}_{1}}-1}-\frac{1}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1})+(\frac{1}{{4}^{{x}_{2}}-1}-\frac{1}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1})]$
=$\frac{1}{2}$$[\frac{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-{4}^{{x}_{1}}}{({4}^{{x}_{1}}-1)({4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1)}+\frac{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-{4}^{{x}_{2}}}{({4}^{{x}_{2}}-1)({4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1)}]$
=$\frac{1}{2}•\frac{{4}^{\frac{{x}_{2}}{2}}-{4}^{\frac{{x}_{1}}{2}}}{{4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1}•\frac{{4}^{{x}_{2}}-{4}^{{x}_{1}}}{({4}^{{x}_{1}}-1)({4}^{{x}_{2}}-1)}$;
可设x2>x1,x1>0,x2>0,则:
${4}^{\frac{{x}_{2}}{2}}-{4}^{\frac{{x}_{1}}{2}}>0,{4}^{{x}_{2}}-{4}^{{x}_{1}}>0$,${4}^{\frac{{x}_{1}+{x}_{2}}{2}}-1>0,({4}^{{x}_{1}}-1)({4}^{{x}_{2}}-1)>0$;
∴$\frac{f({x}_{1})+f({x}_{2})}{2}>f(\frac{{x}_{1}+{x}_{2}}{2})$.
点评 考查奇函数的定义,注意遇到分式的情况,一般需通分处理,以及作差法比较两个函数值的大小,其过程一般是提取公因式,然后把作差的结果和0比较即可.

 名校课堂系列答案
名校课堂系列答案| A. | $\sqrt{2}$(2n-1) | B. | 2(2n-1) | C. | $\frac{\sqrt{2}({4}^{n}-1)}{3}$ | D. | $\frac{2({4}^{n}-1)}{3}$ |
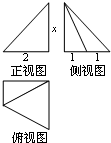 某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )
某几何体的三视图如图所示,且该几何体的体积是6,则正视图中的x的值是( )| A. | 9 | B. | 8 | C. | 3 | D. | 6 |
 已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45°
已知正四棱锥P-ABCD中,AB=6cm,侧面与底面ABCD所成角的大小为45° 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示.