题目内容
判断下列函数的奇偶性.
(1) ;
;
(2) .
.
解:(1)由题意知,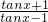 >0,∴tanx>1 或tanx<-1,∴x>kπ+
>0,∴tanx>1 或tanx<-1,∴x>kπ+ 或 x<kπ-
或 x<kπ- ,
,
定义域关于原点对称,设g(x)= ; 则 g(-x)=lg
; 则 g(-x)=lg =lg
=lg
=-lg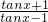 =-g(x),∴g(x)=
=-g(x),∴g(x)= 是奇函数.
是奇函数.
(2)函数定义域是实数集,f(-x)=lg(sin(-x)+ )=lg(
)=lg( -sinx)
-sinx)
=lg =-lg(sinx+
=-lg(sinx+ )=-f(x).∴函数
)=-f(x).∴函数 是奇函数.
是奇函数.
分析:(1) 自变量的取值范围:x>kπ+ 或 x<kπ-
或 x<kπ- ,,定义域关于原点对称,再利用对数的运算性质,得到g(-x)=-g(x),g(x)是奇函数.
,,定义域关于原点对称,再利用对数的运算性质,得到g(-x)=-g(x),g(x)是奇函数.
(2)函数定义域是实数集,关于原点对称,再利用对数的运算性质,f(-x)=-f(x),f(x)是奇函数.
点评:本题考查判断函数奇偶性的方法:先看函数的定义域手否关于原点对称,再看f(-x)与f(x)的关系,依据奇偶函数的定义进行判断.
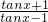 >0,∴tanx>1 或tanx<-1,∴x>kπ+
>0,∴tanx>1 或tanx<-1,∴x>kπ+ 或 x<kπ-
或 x<kπ- ,
,定义域关于原点对称,设g(x)=
 ; 则 g(-x)=lg
; 则 g(-x)=lg =lg
=lg
=-lg
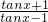 =-g(x),∴g(x)=
=-g(x),∴g(x)= 是奇函数.
是奇函数.(2)函数定义域是实数集,f(-x)=lg(sin(-x)+
 )=lg(
)=lg( -sinx)
-sinx)=lg
 =-lg(sinx+
=-lg(sinx+ )=-f(x).∴函数
)=-f(x).∴函数 是奇函数.
是奇函数.分析:(1) 自变量的取值范围:x>kπ+
 或 x<kπ-
或 x<kπ- ,,定义域关于原点对称,再利用对数的运算性质,得到g(-x)=-g(x),g(x)是奇函数.
,,定义域关于原点对称,再利用对数的运算性质,得到g(-x)=-g(x),g(x)是奇函数.(2)函数定义域是实数集,关于原点对称,再利用对数的运算性质,f(-x)=-f(x),f(x)是奇函数.
点评:本题考查判断函数奇偶性的方法:先看函数的定义域手否关于原点对称,再看f(-x)与f(x)的关系,依据奇偶函数的定义进行判断.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目