题目内容
已知函数 .
.
(I)求f(x)的最小正周期和最大值;
(Ⅱ)在给出的坐标系中画出函数y=f(x)在[0,π]上的图象,并说明y=f(x)的图象是由y=sin2x的图象怎样变换得到的.
解:(I) 函数
=2 (cosxcos
(cosxcos -sinxsin
-sinxsin )(cosxcos
)(cosxcos +sinxsin
+sinxsin )+
)+ sin2x
sin2x
=2 (
( cos2x-
cos2x- sin2x)+
sin2x)+ sin2x=
sin2x= cos2x+
cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ).
).
故f(x)的最小正周期为 =π,最大值为2.
=π,最大值为2.
(Ⅱ)列表:
如图所示:

把y=sin2x的图象向左平移 个单位,再把所得图象上所有的点的纵坐标变为原来的2倍,横坐标不变,即得函数f(x)的图象.
个单位,再把所得图象上所有的点的纵坐标变为原来的2倍,横坐标不变,即得函数f(x)的图象.
分析:(I)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+ ),由此可得它的最小正周期及最大值.
),由此可得它的最小正周期及最大值.
(Ⅱ)用五点法作出函数y=2sin(2x+ )在一个周期上的图象.
)在一个周期上的图象.
点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和最值,用五点法作出函数y=Asin(ωx+φ)在一个周期上的图象,属于中档题.

=2
 (cosxcos
(cosxcos -sinxsin
-sinxsin )(cosxcos
)(cosxcos +sinxsin
+sinxsin )+
)+ sin2x
sin2x =2
 (
( cos2x-
cos2x- sin2x)+
sin2x)+ sin2x=
sin2x= cos2x+
cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ).
).故f(x)的最小正周期为
 =π,最大值为2.
=π,最大值为2.(Ⅱ)列表:
| x | 0 |  |  |  |  | |
2x+ |  |  | π |  | 2π | 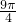 |
| f(x) |  | 2 | 0 | -2 | 0 |  |

把y=sin2x的图象向左平移
 个单位,再把所得图象上所有的点的纵坐标变为原来的2倍,横坐标不变,即得函数f(x)的图象.
个单位,再把所得图象上所有的点的纵坐标变为原来的2倍,横坐标不变,即得函数f(x)的图象.分析:(I)利用三角函数的恒等变换化简函数f(x)的解析式为2sin(2x+
 ),由此可得它的最小正周期及最大值.
),由此可得它的最小正周期及最大值.(Ⅱ)用五点法作出函数y=2sin(2x+
 )在一个周期上的图象.
)在一个周期上的图象.点评:本题主要考查三角函数的恒等变换及化简求值,三角函数的周期性和最值,用五点法作出函数y=Asin(ωx+φ)在一个周期上的图象,属于中档题.

练习册系列答案
相关题目
 .
. .
. .
. =(
=( ,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
,0)平移得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.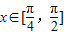 时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.
时,不等式|f(x)-m|<2恒成立,求实数m的取值范围.