题目内容
设函数f(x)=x2+bln(x+1).
(1)若b=﹣4,求函数f(x)的单调区间;
(2)若函数f(x)在定义域上是单调函数,求b的取值范围;
(3)若b=﹣1,证明对任意n∈N+,不等式 …
… 都成立.
都成立.
(1)若b=﹣4,求函数f(x)的单调区间;
(2)若函数f(x)在定义域上是单调函数,求b的取值范围;
(3)若b=﹣1,证明对任意n∈N+,不等式
 …
… 都成立.
都成立.(1)解:求导函数,可得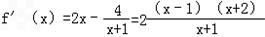 ,定义域{x|x>﹣1}
,定义域{x|x>﹣1}
∴当﹣1<x<1时,f'(x)<0;当x>1时,f'(x)>0.
故函数f(x)的减区间是(﹣1,1),增区间是(1,+∞).
(2)解:∵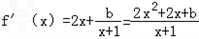 ,
,
又函数f(x)在定义域是单调函数,
∴f'(x)≥0,或f'(x)≤0在(﹣1,+∞)上恒成立.
若f'(x)≥0,∵x+1>0,
∴2x2+2x+b≥0在(﹣1,+∞)上恒成立,即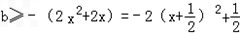 恒成立,
恒成立,
由此得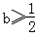 ;
;
若f'(x)≤0,∵x+1>0,
∴2x2+2x+b≤0,即b≤﹣(2x2+2x)恒成立,因﹣(2x2+2x)在(﹣1,+∞)没有最小值,
∴不存在实数b使f'(x)0恒成立.
综上所知,实数b的取值范围是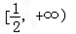 .
.
(3)证明:当b=﹣1时,函数f(x)=x2﹣ln(x+1),
令函数h(x)=f(x)﹣x3=x2﹣ln(x+1)﹣x3,则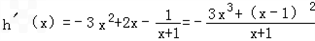 ,
,
∴当x∈[0,+∞)时,h'(x)<0,
∴函数h(x)在[0,+∞)上单调递减,
又h(0)=0,
∴当x∈(0,+∞)时,h(x)<h(0)=0,即x2﹣ln(x+1)<x3恒成立.
故f(x)<x3.
∵k∈N*,∴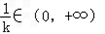 ,
,
取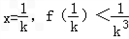 ,
,
∴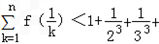 …
…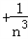 ,
,
故结论成立.
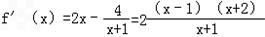 ,定义域{x|x>﹣1}
,定义域{x|x>﹣1}∴当﹣1<x<1时,f'(x)<0;当x>1时,f'(x)>0.
故函数f(x)的减区间是(﹣1,1),增区间是(1,+∞).
(2)解:∵
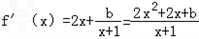 ,
,又函数f(x)在定义域是单调函数,
∴f'(x)≥0,或f'(x)≤0在(﹣1,+∞)上恒成立.
若f'(x)≥0,∵x+1>0,
∴2x2+2x+b≥0在(﹣1,+∞)上恒成立,即
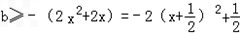 恒成立,
恒成立,由此得
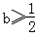 ;
;若f'(x)≤0,∵x+1>0,
∴2x2+2x+b≤0,即b≤﹣(2x2+2x)恒成立,因﹣(2x2+2x)在(﹣1,+∞)没有最小值,
∴不存在实数b使f'(x)0恒成立.
综上所知,实数b的取值范围是
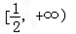 .
.(3)证明:当b=﹣1时,函数f(x)=x2﹣ln(x+1),
令函数h(x)=f(x)﹣x3=x2﹣ln(x+1)﹣x3,则
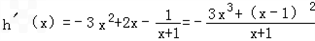 ,
,∴当x∈[0,+∞)时,h'(x)<0,
∴函数h(x)在[0,+∞)上单调递减,
又h(0)=0,
∴当x∈(0,+∞)时,h(x)<h(0)=0,即x2﹣ln(x+1)<x3恒成立.
故f(x)<x3.
∵k∈N*,∴
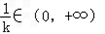 ,
,取
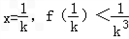 ,
,∴
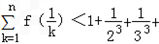 …
…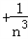 ,
,故结论成立.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目