题目内容
设f（x）=asin2x+bcos2x，其中a，b∈R，ab≠0．若f（x）≤f（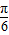
）|对一切x∈R恒成立，则①f（
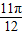）=0；②|f（
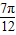）|＜|f（
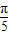）|；③f（x）既不是奇函数也不是偶函数；
④f（x）的单调递增区间是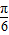[kπ+
，kπ+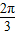
]（k∈Z）；⑤经过点（a，b）的所有直线均与函数f（x）的图象相交．
以上结论正确的是 （写出所有正确结论的编号）．
【答案】分析：化简f（x）的解析式，利用已知条件中的不等式恒成立，得f（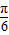
） 是三角函数的最大值，得到x=
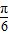是三角函数的对称轴，将其代入整体角令整体角等于kπ+
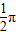，求出辅助角θ，再通过整体处理的思想研究函数的性质．
解答：解：∵f（x）=asin2x+bcos2x=±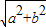
sin（2x+θ）
由f（x）≤f（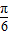
）可得f（
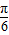）为函数f（x）的最大值
∴2×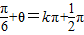
∴
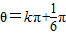
∴f（x）=asin2x+bcos2x=±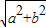
sin（2x+
）
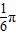对于①f（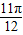
）=
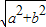sin（2×
+
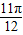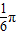）=0；故①对
对于②，|f（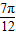
）|=
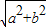|sin（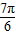
+
）|=
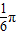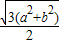
|f（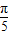
）|=
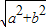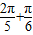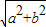|sin（
）|=
|sin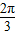
|=
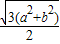
∴|f（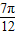
）|＞|f（
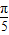）|故②错
对于③，f（x）不是奇函数也不是偶函数，故③正确
对于④，由于f（x）的解析式中有±，故单调性分情况讨论，故④不对
对于⑤要使经过点（a，b）的直线与函数f（x）的图象不相交，则此直线须与横轴平行，且|b|＞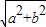
，b2＞a2+b2这不可能，矛盾，故不存在经过点（a，b）的直线于函数f（x）的图象不相交故⑤正确
故答案为：①③⑤
点评：本题考查三角函数的对称轴过三角函数的最值点、考查研究三角函数的性质常用整体处理的思想方法．
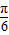） 是三角函数的最大值，得到x= 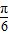是三角函数的对称轴，将其代入整体角令整体角等于kπ+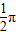，求出辅助角θ，再通过整体处理的思想研究函数的性质．解答：解：∵f（x）=asin2x+bcos2x=±
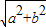sin（2x+θ）由f（x）≤f（
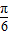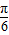）可得f（）为函数f（x）的最大值∴2×
∴
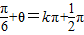
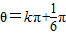
∴f（x）=asin2x+bcos2x=±
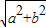sin（2x+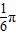）对于①f（
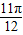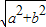）=sin（2×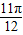+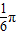）=0；故①对对于②，|f（
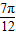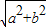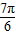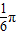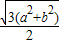
）|=|sin（+）|=|f（
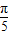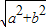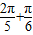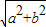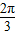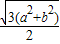
）|=|sin（）|=|sin|=∴|f（
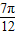）|＞|f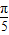（）|故②错对于③，f（x）不是奇函数也不是偶函数，故③正确
对于④，由于f（x）的解析式中有±，故单调性分情况讨论，故④不对
对于⑤要使经过点（a，b）的直线与函数f（x）的图象不相交，则此直线须与横轴平行，且|b|＞
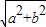，b2＞a2+b2这不可能，矛盾，故不存在经过点（a，b）的直线于函数f（x）的图象不相交故⑤正确故答案为：①③⑤
点评：本题考查三角函数的对称轴过三角函数的最值点、考查研究三角函数的性质常用整体处理的思想方法．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目