题目内容
已知函数 (a为常数).
(a为常数).(1)若常数a<2且a≠0,求f(x)的定义域;
(2)若f(x)在区间(2,4)上是减函数,求a的取值范围.
【答案】分析:(1)由对数函数的性质知其真数必须大于0,对字母a进行分类讨论:当0<a<2时,当a<0时,即可求得求f(x)的定义域;
(2)由题意知函数f(x)是由y= 和
和 复合而来,由复合函数单调性结论,只要u(x)在区间在(2,4)上为增且为正即可.
复合而来,由复合函数单调性结论,只要u(x)在区间在(2,4)上为增且为正即可.
解答:解:(1)由 ,当0<a<2时,解得x<1或
,当0<a<2时,解得x<1或 ,
,
当a<0时,解得 .
.
故当0<a<2时,f(x)的定义域为{x|x<1或 }
}
当a<0时,f(x)的定义域为{x| }.
}.
(2)令 ,因为
,因为 为减函数,
为减函数,
故要使f(x)在(2,4)上是减函数,
则 在(2,4)上为增且为正.
在(2,4)上为增且为正.
故有 .
.
故a∈[1,2).
点评:本题主要考查对数函数的定义域、复合函数的单调性和一元二次方程根的分布,整体思想是解决本类问题的根本.
(2)由题意知函数f(x)是由y=
 和
和 复合而来,由复合函数单调性结论,只要u(x)在区间在(2,4)上为增且为正即可.
复合而来,由复合函数单调性结论,只要u(x)在区间在(2,4)上为增且为正即可.解答:解:(1)由
 ,当0<a<2时,解得x<1或
,当0<a<2时,解得x<1或 ,
,当a<0时,解得
 .
.故当0<a<2时,f(x)的定义域为{x|x<1或
 }
}当a<0时,f(x)的定义域为{x|
 }.
}.(2)令
 ,因为
,因为 为减函数,
为减函数,故要使f(x)在(2,4)上是减函数,
则
 在(2,4)上为增且为正.
在(2,4)上为增且为正.故有
 .
.故a∈[1,2).
点评:本题主要考查对数函数的定义域、复合函数的单调性和一元二次方程根的分布,整体思想是解决本类问题的根本.

练习册系列答案
相关题目
 ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)的图象经过点(1,3).
(a为常数)的图象经过点(1,3). ( a为常数、a∈R),
( a为常数、a∈R), .
. (a为常数)是R上的奇函数,函数
(a为常数)是R上的奇函数,函数
 上恒成立,求t的取值范围
上恒成立,求t的取值范围 其中a为常数,且
其中a为常数,且 .
.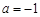 时,求
时,求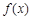 在
在 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域; 对任意
对任意 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.