题目内容
设x>0,y>0,证明不等式: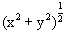 >
>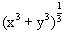 .
.
思路分析:本题含有根式,首先考虑化为整式能否证明,进一步整理,发现可以用基本不等式证明,故采用分析法,当然也可以用综合法.
证明:(分析法)所证不等式即:(x2+y2)3>(x3+y3)2,
即:x6+y6+3x2y2(x2+y2)>x6+y6+2x3y3,
即:3x2y2(x2+y2)>2x3y3,
只需证:x2+y2>![]() xy.
xy.
∵x2+y2≥2xy>![]() xy成立,
xy成立,
∴(x2+y2)![]() >(x3+y3)
>(x3+y3)![]() .
.
(综合法)∵(x2+y2)3=x6+y6+3x2y2(x2+y2)≥x6+y6+6x3y3
>x6+y6+2x3y3=(x3+y3)2,
又∵x>0,y>0,∴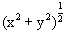 >
>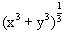 .
.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
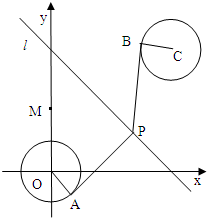 已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|;
已知圆O:x2+y2=1,圆C:(x-4)2+(y-4)2=1,由两圆外一点P(a,b)引两圆切线PA、PB,切点分别为A、B,如图,满足|PA|=|PB|; 中,
中, 平面
平面 ,底面
,底面 .
. 时,求证:
时,求证: ;
; 边上有且只有一个点
边上有且只有一个点 ,使得
,使得 ,求此时二面角
,求此时二面角 的余弦值.
的余弦值.


 ,
, ………………2分
………………2分 ,得证。
,得证。 ,只要
,只要
 ,即
,即 ………6分
………6分
 ,所以
,所以 平面PAD的法向量
平面PAD的法向量
 的大小与二面角A-PD-Q的大小相等所以
的大小与二面角A-PD-Q的大小相等所以

 ………………3分
………………3分

 .
.