题目内容
若α是第二象限的角,且sinα=
,则cosα=
| 2 |
| 3 |
-
| ||
| 3 |
-
.
| ||
| 3 |
分析:根据α是第二象限角得到cosα小于0,然后根据所给的角的正弦值和同角三角函数间的基本关系求出cosα的值即可.
解答:解:因为α是第二象限角,所以cosα<0,
则cosα=-
=-
=-
.
故答案为-
则cosα=-
| 1-sin2α |
1-(
|
| ||
| 3 |
故答案为-
| ||
| 3 |
点评:本题考查同角三角函数间的基本关系化简求值.本题解题的关键是做题时注意角的范围,若题目中没有给出角的范围,则要分类讨论.

练习册系列答案
相关题目
 ,
, .
. 的最大值和最小正周期;
的最大值和最小正周期; ,
, 是第二象限的角,求
是第二象限的角,求 .
. 的最小正周期是
的最小正周期是 ,其中ω>0.
,其中ω>0. ,α是第二象限的角,求sin2α.
,α是第二象限的角,求sin2α. 的最小正周期是
的最小正周期是 ,其中ω>0.
,其中ω>0. ,α是第二象限的角,求sin2α.
,α是第二象限的角,求sin2α. .(1)求
.(1)求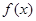 的最大值和最小正周期;(2) 若
的最大值和最小正周期;(2) 若 ,
, 是第二象限的角,求
是第二象限的角,求 .
.