题目内容
在锐角三角形ABC中，角A，B，C的对边分别为a，b，c，且acosC，bcosB，ccosA成等差数列．
（1）求角B的大小；
（2）求2sin2A+cos（A-C）的取值范围．
解、（1）∵2bcosB=acosC+ccosA，∴2sinBcosB=sinAcosC+cosAsinC．（2分）
∴2sinBcosB=sin（A+C），又∵A+C=π-B0＜B＜π，
∴
，即 
．（4分）
（2）由（1）得：
，，△ABC为锐角三角形，
则
，∴
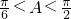．（6分）
=
．（8分）
∵
，
∴
，
即2sin2A+cos（A-C）
．（12分）
分析：（1）利用正弦定理、等差数列的定义和性质以及诱导公式可得，由此求得角B的大小．
（2）三角函数的恒等变换把要求的式子化为，根据角A的范围，求出的
范围．
点评：本题主要考查正弦定理可得以及诱导公式，三角函数的恒等变换及化简求值，等差数列的定义和性质，属于中档题．
∴2sinBcosB=sin（A+C），又∵A+C=π-B0＜B＜π，
∴
，即 ．（4分）（2）由（1）得：
，，△ABC为锐角三角形，则
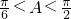，∴．（6分）=．（8分）∵
，∴
，即2sin2A+cos（A-C）
．（12分）分析：（1）利用正弦定理、等差数列的定义和性质以及诱导公式可得
，由此求得角B的大小．（2）三角函数的恒等变换把要求的式子化为
，根据角A的范围，求出的范围．
点评：本题主要考查正弦定理可得以及诱导公式，三角函数的恒等变换及化简求值，等差数列的定义和性质，属于中档题．
练习册系列答案
相关题目