题目内容
(本题满分10分)对于正整数 ≥2,用
≥2,用 表示关于
表示关于 的一元二次方程
的一元二次方程 有实数根的有序数组
有实数根的有序数组 的组数,其中
的组数,其中 (
( 和
和 可以相等);对于随机选取的
可以相等);对于随机选取的 (
( 和
和 可以相等),记
可以相等),记 为关于
为关于 的一元二次方程
的一元二次方程 有实数根的概率。(1)求
有实数根的概率。(1)求 和
和 ;(2)求证:对任意正整数
;(2)求证:对任意正整数 ≥2,有
≥2,有 .
.
【答案】


【解析】 [必做题]本小题主要考查概率的基本知识和记数原理,考查探究能力。满分10分。
(1)因为方程 有实数根,所以
有实数根,所以 。
。
当 时,有
时,有 ,又b
,又b ,故总有
,故总有 ,此时a有
,此时a有 种取法,b有n2种取法,所以共有
种取法,b有n2种取法,所以共有 组有序数组(a,b)满足条件。
组有序数组(a,b)满足条件。
当 时,满足
时,满足 的b有a2个,故共有
的b有a2个,故共有 组有序数组(a,b)满足条件。
组有序数组(a,b)满足条件。

(2)我们只需证明:对于随机选取的a,b ,方程
,方程 无实数根的概率
无实数根的概率 。若方程
。若方程 无实数根,则
无实数根,则 ,由
,由 。因此,满足
。因此,满足 的有序数组(a,b)的组数小于
的有序数组(a,b)的组数小于 ,从而,方程
,从而,方程 无实数根的概率
无实数根的概率 。所以
。所以 。
。

练习册系列答案
相关题目
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
24 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
|
1 |
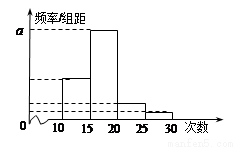
(Ⅰ)求出表中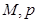 及图中
及图中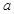 的值;
的值;
(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间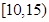 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间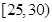 内的概率.
内的概率.
 ,
,
 在
在 处与直线
处与直线 相切;
相切; 的值;②求函数
的值;②求函数 上的最大值;
上的最大值; 时,若不等式
时,若不等式 对所有的
对所有的 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.




 ,
, .
. ,求
,求 值;
值; 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,
, 的取值范围.
的取值范围. 的内角A、B、C所对的边长分别为
的内角A、B、C所对的边长分别为 ,且
,且 ,
, 。
。 时,求
时,求 的值.
的值. 的值.
的值.