��Ŀ����
����֪����y=ax(a��0��a��1)��y=logax(a��0��a��1)��Ϊ��������ֻҪ������һ������ָ�Ի������Ϳ��Եõ����ķ������Ľ���ʽ������һ������y=f(x)����x��y��ʾ�����ܷ�õ����ķ��������ݺ����Ķ��壺�����Ա���x��ÿһ��ֵy����Ψһȷ����ֵ��֮��Ӧ��������ڷ�������Ӧ�Ƕ���y��ÿһ��ֵ��x����Ψһȷ����ֵ��֮��Ӧ���ݴ�̽�����к����Ƿ���ڷ����������ǣ���������ʲô������Ϊʲô��
(1)y=2x+1��
(2)y=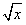 ��
��
(3)y=x2��
(4)y=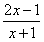 ��
��
(1)y=2x+1��
(2)y=
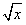 ��
�� (3)y=x2��
(4)y=
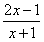 ��
�� �⣺(1)��y=2x+1�ǵ�������������y=2x+1���x=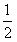 (y-1)��
(y-1)��
��ʱ������y��R������Ψһȷ����x��֮��Ӧ��Ҳ����x��y�ĺ�����
��ϰ����x��ʾ�Ա�����y��ʾ������
��y=2x+1�ķ�����Ϊy=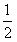 (x-1)��
(x-1)��
(2)ͬ(1)�ĵ�������y=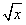 ��������Ҳ���ڷ���������y=
��������Ҳ���ڷ���������y=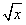 ���x=y2��
���x=y2��
��y=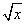 �ķ�����Ϊy=x2����Ϊ�����x����y=
�ķ�����Ϊy=x2����Ϊ�����x����y=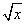 �е�y��y��0��
�е�y��y��0��
��x��0����������Ϊy=x2(x��0)��
(3)��x=��1ʱ������y=1������������y=1��x������ֵ��֮��Ӧ����y=x2�����ڷ�������
(4)��y=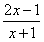 �����x=
�����x=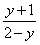 ��
��
��y��ÿһ��ֵ��x����Ψһֵ��֮��Ӧ��
�ʴ��ڷ�������������Ϊy=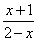 (x��2)��
(x��2)��
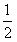 (y-1)��
(y-1)����ʱ������y��R������Ψһȷ����x��֮��Ӧ��Ҳ����x��y�ĺ�����
��ϰ����x��ʾ�Ա�����y��ʾ������
��y=2x+1�ķ�����Ϊy=
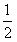 (x-1)��
(x-1)�� (2)ͬ(1)�ĵ�������y=
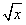 ��������Ҳ���ڷ���������y=
��������Ҳ���ڷ���������y=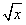 ���x=y2��
���x=y2����y=
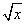 �ķ�����Ϊy=x2����Ϊ�����x����y=
�ķ�����Ϊy=x2����Ϊ�����x����y=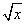 �е�y��y��0��
�е�y��y��0�� ��x��0����������Ϊy=x2(x��0)��
(3)��x=��1ʱ������y=1������������y=1��x������ֵ��֮��Ӧ����y=x2�����ڷ�������
(4)��y=
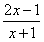 �����x=
�����x=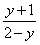 ��
����y��ÿһ��ֵ��x����Ψһֵ��֮��Ӧ��
�ʴ��ڷ�������������Ϊy=
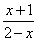 (x��2)��
(x��2)�� 
��ϰ��ϵ�д�
 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
�����Ŀ