题目内容
△ABC中,角A、B、C所对边分别是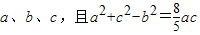 .
.(1)求cos(A+C)+sin2B的值;
(2)若b=2,求△ABC面积的最大值.
【答案】分析:(1)△ABC中,由余弦定理求得cosB的值,利用同角三角函数的基本关系求得sinB的值,再利用二倍角公式、诱导
公式求出cos(A+C)+sin2B的值.
(2)若b=2,则由题意可得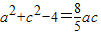 ,利用基本不等式求得ac≤10,再由△ABC面积为
,利用基本不等式求得ac≤10,再由△ABC面积为 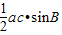 求出
求出
它的最大值.
解答:解:(1)△ABC中,由余弦定理可得 cosB=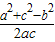 =
= ,
,
∴sinB= ,cos(A+C)+sin2B=-cosB+2sinBcosB=-
,cos(A+C)+sin2B=-cosB+2sinBcosB=- +2×
+2× ×
× =
=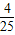 .
.
(2)若b=2,则由题意可得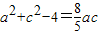 ,
,
∴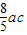 ≥2ac-4,ac≤10,当且仅当 a=c时取等号.
≥2ac-4,ac≤10,当且仅当 a=c时取等号.
故△ABC面积为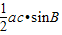 ≤
≤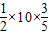 =3,故△ABC面积的最大值为 3.
=3,故△ABC面积的最大值为 3.
点评:本题主要考查余弦定理、二倍角公式、诱导公式、同角三角函数的基本关系、基本不等式的应用,属于中档题.
公式求出cos(A+C)+sin2B的值.
(2)若b=2,则由题意可得
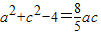 ,利用基本不等式求得ac≤10,再由△ABC面积为
,利用基本不等式求得ac≤10,再由△ABC面积为 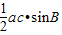 求出
求出它的最大值.
解答:解:(1)△ABC中,由余弦定理可得 cosB=
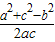 =
= ,
,∴sinB=
 ,cos(A+C)+sin2B=-cosB+2sinBcosB=-
,cos(A+C)+sin2B=-cosB+2sinBcosB=- +2×
+2× ×
× =
=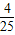 .
.(2)若b=2,则由题意可得
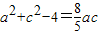 ,
,∴
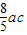 ≥2ac-4,ac≤10,当且仅当 a=c时取等号.
≥2ac-4,ac≤10,当且仅当 a=c时取等号.故△ABC面积为
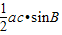 ≤
≤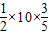 =3,故△ABC面积的最大值为 3.
=3,故△ABC面积的最大值为 3.点评:本题主要考查余弦定理、二倍角公式、诱导公式、同角三角函数的基本关系、基本不等式的应用,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目