题目内容
函数y=tan(x+ )的单调递增区间是
)的单调递增区间是
- A.(-
 +kπ,
+kπ, +kπ),k∈Z
+kπ),k∈Z - B.(-
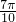 +kπ,
+kπ, +kπ),k∈Z
+kπ),k∈Z - C.(-
 +kπ,
+kπ,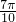 +kπ),k∈Z
+kπ),k∈Z - D.(-
 +kπ,
+kπ, +kπ),k∈Z
+kπ),k∈Z
C
分析:由y=tanx的单调递增区间为(kπ- ,kπ+
,kπ+ )(k∈Z),把x+
)(k∈Z),把x+ 整体代入解不等式可得答案.
整体代入解不等式可得答案.
解答:∵y=tanx的单调递增区间为(kπ- ,kπ+
,kπ+ )(k∈Z),
)(k∈Z),
令kπ- <x+
<x+ <kπ+
<kπ+ ,解得kπ-
,解得kπ-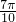 <x<kπ+
<x<kπ+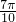 ,
,
∴函数y=tan(x+ )的单调递增区间是(kπ-
)的单调递增区间是(kπ-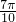 ,kπ+
,kπ+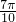 )(k∈Z),
)(k∈Z),
故选C
点评:本题考查正切函数的单调性,着重考查整体代换的数学思想,属于中档题.
分析:由y=tanx的单调递增区间为(kπ-
 ,kπ+
,kπ+ )(k∈Z),把x+
)(k∈Z),把x+ 整体代入解不等式可得答案.
整体代入解不等式可得答案.解答:∵y=tanx的单调递增区间为(kπ-
 ,kπ+
,kπ+ )(k∈Z),
)(k∈Z),令kπ-
 <x+
<x+ <kπ+
<kπ+ ,解得kπ-
,解得kπ-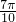 <x<kπ+
<x<kπ+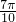 ,
,∴函数y=tan(x+
 )的单调递增区间是(kπ-
)的单调递增区间是(kπ-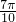 ,kπ+
,kπ+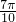 )(k∈Z),
)(k∈Z),故选C
点评:本题考查正切函数的单调性,着重考查整体代换的数学思想,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
若将函数y=tan(ωx+
)(ω>0)的图象向右平移
个单位长度后,与函数y=tan(ωx+
)的图象重合,则ω的最小值为( )
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果函数y=tan(x+φ)的图象经过点(
, 0),那么φ可以是( )
| π |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|