题目内容
已知函数f(x)=3-2log2x,g(x)=log2x.(1)求函数
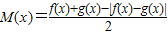 的最大值;
的最大值;(2)如果对f(x2)f(
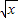 )>kg(x)中的任意x∈[1,4],不等式恒成立,求实数k的取值范围.
)>kg(x)中的任意x∈[1,4],不等式恒成立,求实数k的取值范围.
【答案】分析:(1)先将绝对值符号化去,再确定函数的最大值;
(2)令t=log2x,将对f(x2)f(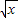 )>kg(x)中的任意x∈[1,4]不等式恒成立,转化为(3-4t)(3-t)>kt对一切t∈[0,2]恒成立,分类讨论,利用分离参数法,即可求实数k的取值范围.
)>kg(x)中的任意x∈[1,4]不等式恒成立,转化为(3-4t)(3-t)>kt对一切t∈[0,2]恒成立,分类讨论,利用分离参数法,即可求实数k的取值范围.
解答:解:(1)f(x)-g(x)=3(1-log2x),
当x>2时,f(x)<g(x);当0<x≤2时,f(x)≥g(x),
∴M(x)=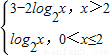
当0<x≤2时,M(x)的最大值为1;当x>2时,M(x)<1.
综上:当x=2时,M(x)取到最大值为1.
(2)由f(x2)f(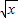 )>kg(x)得:(3-4log2x)(3-log2x)>k•log2x,
)>kg(x)得:(3-4log2x)(3-log2x)>k•log2x,
令t=log2x,∵x∈[1,4],∴t∈[0,2],
∴(3-4t)(3-t)>kt对一切t∈[0,2]恒成立.
①当t=0时,k∈R;
②当t∈(0,2]时,k<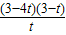 恒成立,即k<4t+
恒成立,即k<4t+ -15,
-15,
∵4t+ ≥12,当且仅当4t=
≥12,当且仅当4t= ,即t=
,即t= 时取等号.
时取等号.
∴4t+ -15的最小值为-3,∴k<-3.
-15的最小值为-3,∴k<-3.
综上k的取值范围是k<-3.
点评:本题考查函数的最值,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.
(2)令t=log2x,将对f(x2)f(
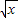 )>kg(x)中的任意x∈[1,4]不等式恒成立,转化为(3-4t)(3-t)>kt对一切t∈[0,2]恒成立,分类讨论,利用分离参数法,即可求实数k的取值范围.
)>kg(x)中的任意x∈[1,4]不等式恒成立,转化为(3-4t)(3-t)>kt对一切t∈[0,2]恒成立,分类讨论,利用分离参数法,即可求实数k的取值范围.解答:解:(1)f(x)-g(x)=3(1-log2x),
当x>2时,f(x)<g(x);当0<x≤2时,f(x)≥g(x),
∴M(x)=
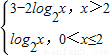
当0<x≤2时,M(x)的最大值为1;当x>2时,M(x)<1.
综上:当x=2时,M(x)取到最大值为1.
(2)由f(x2)f(
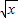 )>kg(x)得:(3-4log2x)(3-log2x)>k•log2x,
)>kg(x)得:(3-4log2x)(3-log2x)>k•log2x,令t=log2x,∵x∈[1,4],∴t∈[0,2],
∴(3-4t)(3-t)>kt对一切t∈[0,2]恒成立.
①当t=0时,k∈R;
②当t∈(0,2]时,k<
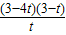 恒成立,即k<4t+
恒成立,即k<4t+ -15,
-15,∵4t+
 ≥12,当且仅当4t=
≥12,当且仅当4t= ,即t=
,即t= 时取等号.
时取等号.∴4t+
 -15的最小值为-3,∴k<-3.
-15的最小值为-3,∴k<-3.综上k的取值范围是k<-3.
点评:本题考查函数的最值,考查恒成立问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=3•2x-1,则当x∈N时,数列{f(n+1)-f(n)}( )
| A、是等比数列 | B、是等差数列 | C、从第2项起是等比数列 | D、是常数列 |