题目内容
复数z=x+yi（其中x，y∈R）满足方程|z-1|=2|
|，则在复平面上z表示的图形是
. | z |
圆
圆
．分析：由题意把|z-1|=2|
|平方可得关于xy的方程，化简方程可判其对应的图形．
. |
| z |
解答：解：∵z=x+yi，|z-1|=2|
|，
∴|z-1|2=（2|
|）2，
∴|x-1+yi|2=（2|x-yi|）2，
∴（x-1）2+y2=4[x2+（-y）2]，
化简可得3x2+3y2+2x-1=0，
可得22+02-4×3×（-1）=16＞0，
故该方程表示的图形为圆，
故答案为：圆
. |
| z |
∴|z-1|2=（2|
. |
| z |
∴|x-1+yi|2=（2|x-yi|）2，
∴（x-1）2+y2=4[x2+（-y）2]，
化简可得3x2+3y2+2x-1=0，
可得22+02-4×3×（-1）=16＞0，
故该方程表示的图形为圆，
故答案为：圆
点评：本题考查复数的代数形式及其几何意义，涉及复数的模长公式，属基础题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
＝ad－bc，若复数z＝x＋yi(x、y∈R)，满足
的模等于x，则复数z对应的z(x，y)的轨迹方程为________；其图形为________．
．
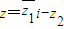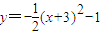上运动，求复数z所对应的点P（x，y）的轨迹方程；
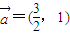方向平移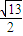
个单位，得到新的轨迹C，求C的轨迹方程；