题目内容
已知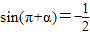
，计算：（1）sin（5π-α）；
（2）
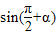；（3）
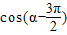；（4）
．
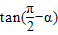【答案】分析：先由公式sin（π+α）=-sinα求出sinα的值：
（1）由公式sin（α+2kπ）=sinα及sin（π-α）=sinα解之；（2）由公式sin（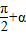
）=cosα及sin2α+cos2α=1解之；
（3）由公式cos（α+2kπ）=cosα及cos（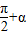
）=-sinα解之；
（4）由公式tanα=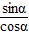
及sin（
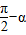）=cosα、cos（
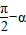）=sinα解之．
解答：解：因为sin（π+α）=-
，所以-sinα=-
，即sinα=
，
（1）sin（5π-α）=sin（π-α）=sinα=
；
（2）sin（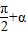
）=cosα=
=
；
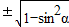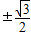（3）cos（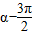
）=cos（
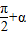）=-sinα=-
；
（4）tan（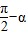
）=
=
=
．
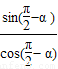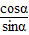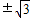点评：本题主要考查诱导公式．
（1）由公式sin（α+2kπ）=sinα及sin（π-α）=sinα解之；（2）由公式sin（
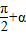）=cosα及sin2α+cos2α=1解之；（3）由公式cos（α+2kπ）=cosα及cos（
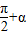）=-sinα解之；（4）由公式tanα=
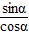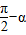及sin（）=cosα、cos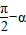（）=sinα解之．解答：解：因为sin（π+α）=-
，所以-sinα=-，即sinα=，（1）sin（5π-α）=sin（π-α）=sinα=
；（2）sin（
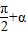）=cosα=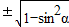=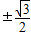；（3）cos（
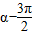）=cos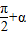（）=-sinα=-；（4）tan（
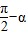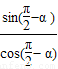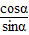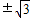）===．点评：本题主要考查诱导公式．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
一半径为2m的水轮如图所示，水轮圆心O距离水面1m；已知水轮按逆时针做匀速转动，每3s转一圈，如果当水轮上点P从水中浮现时（图中点P0）开始计算时间．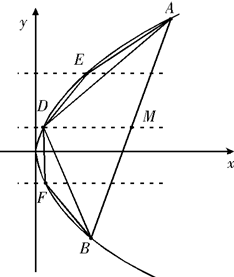
（2007•浦东新区二模）已知抛物线C：y2=2px（p＞0）上横坐标为4的点到焦点的距离为5．
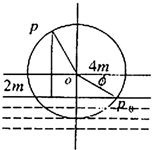如图，一个水轮的半径为4m，水轮圆心O距离水面2m，已知水轮每分钟转动5圈，如果当水轮上点P从水中浮现时（图中点p0）开始计算时间．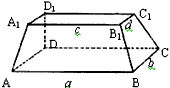
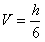（S上底面+4S中截面+S下底面），试判断V估与V的大小关系，并加以证明。
终边相同角的集合S，并且把S中适合不等式-2π≤β＜4π的元素β写出来．
，计算
．