题目内容
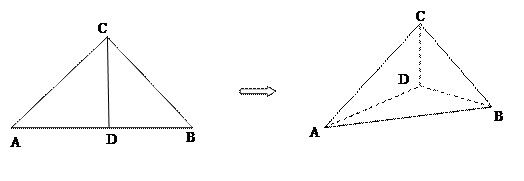
(本题满分12分 )如图,在等腰直角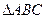 中,
中,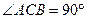 ,
,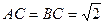 ,
,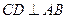 ,
,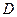 为垂足.沿
为垂足.沿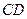 将
将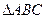 对折,连结
对折,连结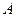 、
、 ,使得
,使得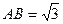 .
.
(1)对折后,在线段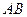 上是否存在点
上是否存在点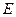 ,使
,使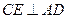 ?若存在,求出
?若存在,求出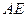 的长;若不存在,说明理由;
的长;若不存在,说明理由;
(2)对折后,求二面角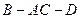 的平面角的大小.
的平面角的大小.
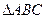 中,
中,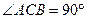 ,
,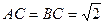 ,
,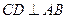 ,
,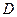 为垂足.沿
为垂足.沿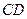 将
将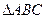 对折,连结
对折,连结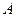 、
、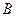 ,使得
,使得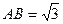 .
.
(1)对折后,在线段
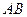 上是否存在点
上是否存在点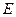 ,使
,使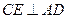 ?若存在,求出
?若存在,求出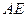 的长;若不存在,说明理由;
的长;若不存在,说明理由; (2)对折后,求二面角
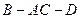 的平面角的大小.
的平面角的大小.(1)在线段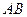 上存在点
上存在点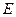 ,使
,使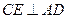 ; (2)
; (2)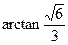
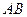 上存在点
上存在点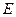 ,使
,使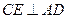 ; (2)
; (2)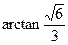
解:(1)在线段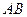 上存在点
上存在点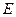 ,使
,使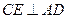 .
.

由等腰直角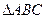 可知,对折后,
可知,对折后,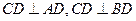 ,
,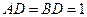 .
.
在 中,
中,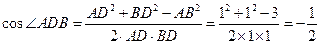 ,
,
∴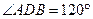 ,
,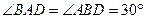 .
.
过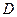 作
作 的垂线,与
的垂线,与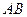 的交于点
的交于点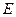 ,点
,点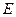 就是
就是
满足条件的唯一点.理由如下:
连结 ,∵
,∵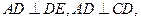
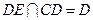 ,∴
,∴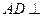 平面
平面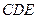 ,
,
∴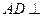
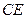 ,即在线段
,即在线段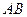 上存在点
上存在点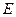 ,使
,使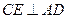 . ………………4分
. ………………4分
在 中,
中,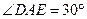 ,
, ,得
,得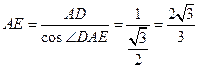 .……6分
.……6分
(2)对折后,作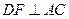 于
于 ,连结
,连结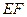 ,
,
∵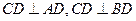 ,
,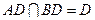 ,
,
∴ 平面
平面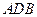 ,
,
∴平面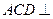 平面
平面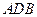 .
.
∵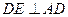 ,且平面
,且平面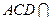 平面
平面 ,
,
∴ 平面
平面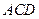 .
.
而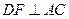 ,所以
,所以 平面
平面 ,
,
即 为二面角
为二面角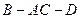 的平面角. ……………………9分
的平面角. ……………………9分
在 中,
中,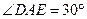 ,
, ,
,
得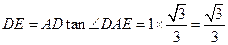 ,
,
在 中,
中,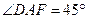 ,
, ,得
,得
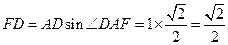 .
.
在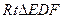 中,
中,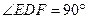 ,
,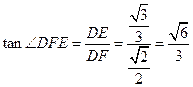 ,
,
所以二面角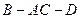 的大小为
的大小为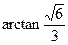 . ……………………12分
. ……………………12分
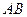 上存在点
上存在点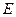 ,使
,使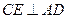 .
. 
由等腰直角
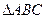 可知,对折后,
可知,对折后,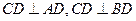 ,
,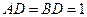 .
.在
 中,
中,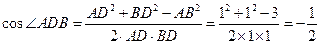 ,
,∴
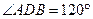 ,
,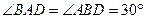 .
. 过
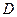 作
作 的垂线,与
的垂线,与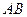 的交于点
的交于点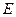 ,点
,点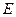 就是
就是 满足条件的唯一点.理由如下:
连结
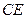 ,∵
,∵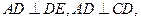
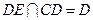 ,∴
,∴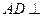 平面
平面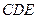 ,
,∴
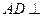
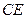 ,即在线段
,即在线段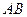 上存在点
上存在点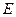 ,使
,使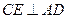 . ………………4分
. ………………4分 在
 中,
中,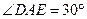 ,
, ,得
,得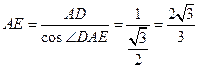 .……6分
.……6分(2)对折后,作
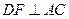 于
于 ,连结
,连结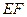 ,
,∵
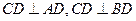 ,
,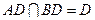 ,
,∴
 平面
平面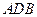 ,
,∴平面
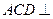 平面
平面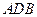 .
. ∵
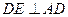 ,且平面
,且平面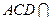 平面
平面 ,
,∴
 平面
平面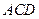 .
.而
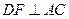 ,所以
,所以 平面
平面 ,
,即
 为二面角
为二面角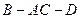 的平面角. ……………………9分
的平面角. ……………………9分在
 中,
中,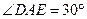 ,
, ,
,得
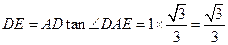 ,
,在
 中,
中,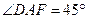 ,
, ,得
,得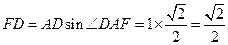 .
. 在
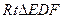 中,
中,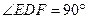 ,
,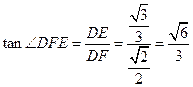 ,
, 所以二面角
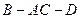 的大小为
的大小为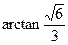 . ……………………12分
. ……………………12分 
练习册系列答案
相关题目

 ,侧面积为
,侧面积为
 ,则此圆锥的体积为__________
,则此圆锥的体积为__________
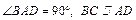 ,且PA=AB=BC=1,AD=2.
,且PA=AB=BC=1,AD=2.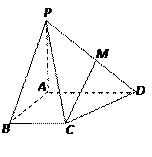
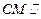 平面PAB;
平面PAB; 中,
中,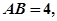 沿对角线
沿对角线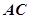 将正方形
将正方形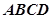 折成一个直二面角
折成一个直二面角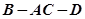 ,则点
,则点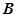 到直线
到直线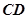 的距离为( )
的距离为( )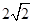
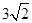
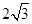
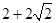
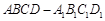 中,棱长都相等;条件乙:直四棱柱
中,棱长都相等;条件乙:直四棱柱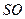 中,
中,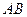 、
、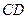 为底面圆的两条直径,
为底面圆的两条直径,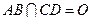 ,且
,且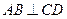 ,
,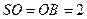 ,
,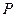 为
为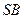 的中点.异面直线
的中点.异面直线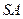 与
与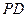 所成角的正切值为 .
所成角的正切值为 .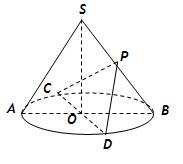
 过点
过点 ,且
,且 是它的一个法向量,则
是它的一个法向量,则