题目内容
三棱锥A-BCD中，AB=CD=a，截面MNPQ与AB、CD都平行，则截面MNPQ的周长是（ ）A．4a
B．2a
C．
D．周长与截面的位置有关
【答案】分析：设M在AC上，N点在BC上，P点在BD上，Q点在AD上，
=k，根据截面MNPQ与AB、CD都平行，可得
=
=
，
=
=
，进而可得截面MNPQ的周长．
解答：
解：设M在AC上，N点在BC上，P点在BD上，Q点在AD上
设
=k，则
∵截面MNPQ与AB、CD都平行
∴MN∥AB，PQ∥AB，MQ∥CD，NP∥CD
∴
=
=
，
=
=
∵AB=CD=a，
∴MN=PQ=
，MQ=NP=
∴截面MNPQ的周长为
MN+PQ+MQ+NP=2（
+
）=2a
故选B
点评：本题考查的知识点是棱锥的结构特征，平行线分线段成比例定理，其中设
=k时，求得
=
=
，
=
=
是解答本题的关键．
=k，根据截面MNPQ与AB、CD都平行，可得==，==，进而可得截面MNPQ的周长．解答：
解：设M在AC上，N点在BC上，P点在BD上，Q点在AD上设
=k，则∵截面MNPQ与AB、CD都平行
∴MN∥AB，PQ∥AB，MQ∥CD，NP∥CD
∴
==，==∵AB=CD=a，
∴MN=PQ=
，MQ=NP=∴截面MNPQ的周长为
MN+PQ+MQ+NP=2（
+）=2a故选B
点评：本题考查的知识点是棱锥的结构特征，平行线分线段成比例定理，其中设
=k时，求得==，==是解答本题的关键． 
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
如图，在三棱锥A-BCD中，E、F、G、H分别是边AB、BC、CD、DA的中点．
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．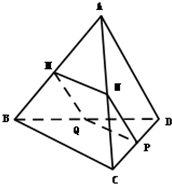
如图，在三棱锥A-BCD中，平行于BC的平面MNPQ分别交AB、AC、CD、BD于M、N、P、Q四点，且MN=PQ．