题目内容
已知n条直线l1:x-y+C1=0,C1=
,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
(1)求Cn;
(2)求x-y+Cn=0与x轴、y轴围成的图形的面积;
(3)求x-y+Cn-1=0与x-y+Cn=0及x轴、y轴围成图形的面积.
| 2 |
(1)求Cn;
(2)求x-y+Cn=0与x轴、y轴围成的图形的面积;
(3)求x-y+Cn-1=0与x-y+Cn=0及x轴、y轴围成图形的面积.
(1)原点O到l1的距离为1,原点O到l2的距离为1+2,原点O到ln的距离dn为1+2++n=
.
∵Cn=
dn,
∴Cn=
.
(2)设直线ln:x-y+Cn=0交x轴于M,交y轴于N,则△OMN面积
S△OMN=
|OM|•|ON|=
Cn2=
.
(3)所围成的图形是等腰梯形,由(2)知Sn=
,则有Sn-1=
.
∴Sn-Sn-1=
-
=n3.
∴所求面积为n3.
| n(n+1) |
| 2 |
∵Cn=
| 2 |
∴Cn=
| ||
| 2 |
(2)设直线ln:x-y+Cn=0交x轴于M,交y轴于N,则△OMN面积
S△OMN=
| 1 |
| 2 |
| 1 |
| 2 |
| n2(n+1)2 |
| 4 |
(3)所围成的图形是等腰梯形,由(2)知Sn=
| n2(n+1)2 |
| 4 |
| (n-1)2•n2 |
| 4 |
∴Sn-Sn-1=
| n2(n+1)2 |
| 4 |
| (n-1)2•n2 |
| 4 |
∴所求面积为n3.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
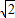 ,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.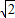 ,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.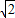 ,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.
,l2:x-y+C2=0,l3:x-y+C3=0,…,ln:x-y+Cn=0(其中C1<C2<C3<…<Cn),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n.