题目内容
11.将甲、乙、丙等六人分配到A,B,C三个社区服务,每个社区2人,要求甲必须在A社区,乙和丙均不能在C社区,则不同的安排种数为9.分析 本题要先安排乙和丙两人,其安排方法可以分为两类,一类是两者之一在A社区,另一个在B社区,另一类是两者都在B社区,在每一类中用分步原理计算种数即可.
解答 解:若乙和丙两人有一人在A社区,另一人在B社区,则第一步安排A社区有2种安排方法,第二步安排B社区,从三人中选一人有三种方法,第二步余下两人去C社区,一种方法;
故此类中安排方法种数是2×3=6,
若乙和丙两人在B社区,第一步安排A社区,有三种安排方法,第二步安排C社区,余下两人去B社区,一种安排方法,故总的安排方法有3×1=3,
综上,总的安排方法种数有6+3=9种;
故答案为:9.
点评 本题考查分步原理与分类原理的应用,求解本题关键是根据实际情况选择正确的分类标准与分步标准,把实际问题的结构理解清楚.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.若命题p:0是偶数,命题q:2是3的约数.则下列命题中为真的是( )
| A. | p且q | B. | p或q | C. | 非p | D. | 非p且非q |
19.如图三角形OAB为用斜二测画法所画的直观图,其原来平面图形的面积是( )
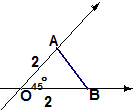

| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
16.已知$tanα=\frac{1}{2}$,则$\frac{{2{{cos}^2}\frac{α}{2}-sinα-1}}{{\sqrt{2}sin(\frac{π}{4}+α)}}$的值为( )
| A. | $\frac{4}{3}$ | B. | -3 | C. | $\frac{1}{3}$ | D. | 3 |
1.椭圆的中心在原点,焦点在x轴上,焦距为4,离心率为$\frac{{\sqrt{2}}}{2}$,则该椭圆的方程为( )
| A. | $\frac{x^2}{32}$+$\frac{y^2}{16}$=1 | B. | $\frac{x^2}{12}$+$\frac{y^2}{8}$=1 | C. | $\frac{x^2}{8}$+$\frac{y^2}{4}$=1 | D. | $\frac{x^2}{12}$+$\frac{y^2}{4}$=1 |