题目内容
(本小题满分12分)
已知椭圆
 的离心率为
的离心率为 ,直线
,直线 经过椭圆的上顶点
经过椭圆的上顶点 和右顶点
和右顶点 ,并且和圆
,并且和圆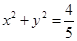 相切.
相切.
(1)求椭圆 的方程;
的方程;
(2)设直线
 与椭圆
与椭圆 相交于
相交于 ,
, 两点,以线段
两点,以线段 ,
,  为邻边作平行四边行
为邻边作平行四边行 ,其中顶点
,其中顶点 在椭圆
在椭圆 上,
上, 为坐标原点,求
为坐标原点,求 的取值范围.
的取值范围.
【答案】
(1)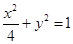
(2)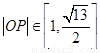
【解析】本试题主要是考查了椭圆方程的求解,以及直线与椭圆的位置关系的综合运用。
(1)因为椭圆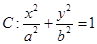
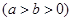 的离心率为
的离心率为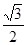 ,直线
,直线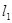 经过椭圆的上顶点
经过椭圆的上顶点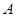 和右顶点
和右顶点 ,并且和圆
,并且和圆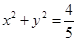 相切.
相切.
结合椭圆的性质和线与圆的位置关系得到参数a,b,c的表达式,得到椭圆的方程。
(2)根据直线方程与椭圆方程联立方程组,结合韦达定理表示出点P的坐标,然后点P在椭圆上得到参数的关系式,,利用m的范围得到op 的范围。
解:(1)由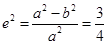 得
得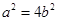 ,所以
,所以 ……………………1分
……………………1分
所以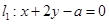 ,有
,有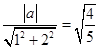 ,解得
,解得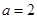 ………..5分
………..5分
所以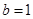 ,所以椭圆方程为
,所以椭圆方程为 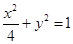 …………………………….6分
…………………………….6分
(2)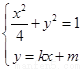 , 消去
, 消去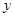 得:
得: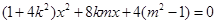
设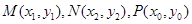
则 ,
, 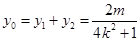 ,
,
故点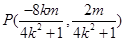 …………………………………………………9分
…………………………………………………9分
点 在椭圆上,有
在椭圆上,有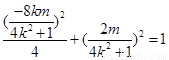 ,整理得
,整理得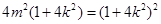
所以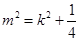 ,
,
而 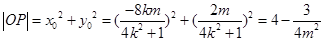 ,………….11分
,………….11分
因为 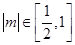 ,所以
,所以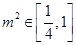 ,所以
,所以
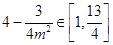 ,
,
所以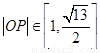 …………………………………………………………….12分
…………………………………………………………….12分

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目