Question

（本小题满分13分）

为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12.

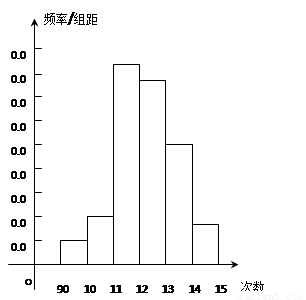
(Ⅰ)第二小组的频率是多少？样本容量是多少？

(Ⅱ)若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？（Ⅲ）在这次测试中，学生跳绳次数的中位数、众数各是是多少？（精确到0.1）

 

Answer 1

【答案】

（I）由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小，

因此第二小组的频率为：

又因为频率=

；

（II）由图可估计该学校高一学生的达标率约为；

（III）跳绳次数的中位数落在第四小组内，中位数为： 120+6÷45×10=121.3。

【解析】

试题分析：（1）根据各个小矩形的面积之比，做出第二组的频率，再根据所给的频数，做出样本容量．

（2）从频率分步直方图中看出次数子啊110以上的频数，用频数除以样本容量得到达标率，进而估计高一全体学生的达标率．

（3）在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数，处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数．

解：（I）由于频率分布直方图以面积的形式反映了数据落在各小组内的频率大小，

因此第二小组的频率为：

又因为频率=

………………（5分）

（II）由图可估计该学校高一学生的达标率约为

………………（8分）

（III）由已知可得各小组的频数依次为6，12，51，45，27，9，所以前三组的频数之和为

69，总频数为150，所以跳绳次数的中位数落在第四小组内，

中位数为： 120+6÷45×10=121.3………………（13分）

考点：本题主要考查了频率分步直方图，考查用样本的频率分布估计总体的频率分布，本题解题的关键是读懂直方图，本题是一个基础题．

点评：解决该试题的关键是看清图中所给的条件，知道小长方形的面积就是这组数据的频率，并利用直方图得到众数和中位数的意义。