题目内容
在平面直角坐标系 中,直线
中,直线 的参数方程为:
的参数方程为: (
(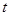 为参数).以坐标原点
为参数).以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的平面直角坐标方程;
的平面直角坐标方程;
(Ⅱ)设直线 与曲线
与曲线 交于点
交于点 ,若点
,若点 的坐标为
的坐标为 ,求
,求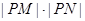 的值.
的值.
(Ⅰ) ;(Ⅱ)
;(Ⅱ) .
.
解析试题分析:(Ⅰ)直接根据极坐标方程与直角坐标的转换关系式 结合三角函数中的两角和与差的三角函数公式即可实现将曲线
结合三角函数中的两角和与差的三角函数公式即可实现将曲线 的参数方程化为直角坐标方程;(Ⅱ)先将直线
的参数方程化为直角坐标方程;(Ⅱ)先将直线 的参数方程与曲线
的参数方程与曲线 的直角坐标方程联立转化为含
的直角坐标方程联立转化为含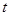 的一元二次方程,然后根据参数方程中的相关理论直接求
的一元二次方程,然后根据参数方程中的相关理论直接求 的值.
的值.
试题解析:(Ⅰ)由 ,得
,得 ,
,
当 时,得
时,得 ,
,
对应直角坐标方程为: .
.
当 ,
, 有实数解,说明曲线
有实数解,说明曲线 过极点,而方程
过极点,而方程 所表示的曲线也过原点.
所表示的曲线也过原点.
∴曲线 的直角坐标方程为
的直角坐标方程为 . 3分
. 3分
(Ⅱ)把直线 的参数方程代入曲线
的参数方程代入曲线 的直角坐标方程,得
的直角坐标方程,得 ,
,
即 ,由于
,由于 ,故可设
,故可设 是上述方程的两实根,
是上述方程的两实根,
则 . 5分
. 5分
∵直线 过点
过点 ,
,
∴由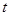 的几何意义,可得
的几何意义,可得 . 7分
. 7分
考点:极坐标与参数方程、韦达定理

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,方向向量为
,方向向量为 的直线,圆方程
的直线,圆方程
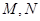 两点,求
两点,求 的值
的值 中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为
中,以O为极点,x轴正半轴为极轴建立极坐标系.曲线C的极坐标方程为 ,M,N分别为C与x轴,y轴的交点.
,M,N分别为C与x轴,y轴的交点. 中,圆
中,圆 的参数方程
的参数方程 为参数).以
为参数).以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.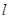 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 ,与直线
,与直线 ,求线段
,求线段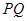 的长.
的长. 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程为
的极坐标方程为 .试求曲线
.试求曲线 的方程为
的方程为 ,以极点为原点,极轴方向为
,以极点为原点,极轴方向为 正半轴方向,利用相同单位长度建立平面直角坐标系,曲线
正半轴方向,利用相同单位长度建立平面直角坐标系,曲线 的参数方程为
的参数方程为 (
( 为参数).
为参数). 的普通方程;
的普通方程; 为曲线
为曲线 的两条切线,求这两条切线所成角余弦值的取值范围.
的两条切线,求这两条切线所成角余弦值的取值范围.  中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
, 为参数),在以
为参数),在以 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 对应的参数
对应的参数 ,射线
,射线 与曲线
与曲线 ,
, ,
, 在曲线
在曲线 的值.
的值. =2
=2 .
. (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值. 的极坐标方程是
的极坐标方程是 ,直线
,直线 的参数方程是
的参数方程是 (
( 为参数).
为参数). 轴的交点是
轴的交点是 为曲线
为曲线 的最大值.
的最大值.