题目内容
顶点在坐标原点,开口向上的抛物线经过点 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
.

(1)求数列{ xn },{ yn}的通项公式 ;
;
(2)设 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;
(3)设 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围.
 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 .
.
(1)求数列{ xn },{ yn}的通项公式
 ;
;(2)设
 ,数列{ an}的前n项和为Tn.求证:
,数列{ an}的前n项和为Tn.求证: ;
;(3)设
 ,若对于任意正整数n,不等式
,若对于任意正整数n,不等式 …
… ≥
≥ 成立,求正数a的取值范围.
成立,求正数a的取值范围. ,
, .(II)见解析 (III)
.(II)见解析 (III)

本试题主要是结合函数的图像来分析数列的通项公式和数列的求和以及数列与不等式的关系的证明。
(1)顶点在坐标原点,开口向上的抛物线经过点 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 ,按照此规律得到通项公式
,按照此规律得到通项公式
(2) 由(1)知 .所以
.所以

 ) .利用裂项求和得到结论。
) .利用裂项求和得到结论。
(3)由于 ,故
,故 .
.
对任意正整数n,不等式 成立,
成立,
即
 恒成立.
恒成立.
因此构造函数
 ,判定函数单调性得到参数的范围。
,判定函数单调性得到参数的范围。
(1)顶点在坐标原点,开口向上的抛物线经过点
 ,过点
,过点 作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点
作抛物线的切线交x轴于点B1,过点B1作x轴的垂线交抛物线于点A1,过点A1作抛物线的切线交x轴于点B2,…,过点 作抛物线的切线交x轴于点
作抛物线的切线交x轴于点 ,按照此规律得到通项公式
,按照此规律得到通项公式(2) 由(1)知
 .所以
.所以

 ) .利用裂项求和得到结论。
) .利用裂项求和得到结论。(3)由于
 ,故
,故 .
.对任意正整数n,不等式
 成立,
成立,即

 恒成立.
恒成立.因此构造函数

 ,判定函数单调性得到参数的范围。
,判定函数单调性得到参数的范围。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象是
的图象是
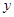 与乘客量
与乘客量 之间关系的图象.由于目前该条公交线路亏损,公司有关人员提出了
之间关系的图象.由于目前该条公交线路亏损,公司有关人员提出了
 的函数关系表示的图象只可能是( )
的函数关系表示的图象只可能是( )

 的图象恒过定点
的图象恒过定点 ,则点
,则点 .
. 的图象;
的图象; 的解集为
的解集为 ,求
,求 值.
值. ,且关于
,且关于 的方程
的方程 有且只有一个实根,则实数
有且只有一个实根,则实数 的范围是( )
的范围是( )



 的部分图象,则函数
的部分图象,则函数 在点(b,g(b))处切线的斜率的最小值是( )
在点(b,g(b))处切线的斜率的最小值是( )


 的图象是( )
的图象是( ) 
