题目内容
（本小题满分12分）如图，在正方体ABCD—A1B1C1D1中，M、N、G分别是A1A，D1C，AD的中点．求证：
（Ⅰ）MN∥平面ABCD；
（Ⅱ）MN⊥平面B1BG．
证明：（1）取CD的中点记为E，连NE，AE．
由N，E分别为CD1与CD的中点可得
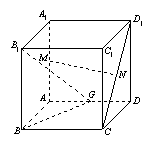NE∥D1D且NE=
D1D，
又AM∥D1D且AM=D1D……3分
所以AM∥EN且AM=EN，即四边形AMNE为平行四边形,所以MN∥AE，
又AE
面ABCD,所以MN∥面ABCD……6分
（２）由AG＝DE ，
，DA＝AB
可得
与
全等,所以
，
又
,
，所以
所以
， …10分
又
,所以
，
又MN∥AE，所以MN⊥平面B1BG ……12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
