题目内容
在平行四边形ABCD中, =
=
 ,
, =
=
 ,CE与BF相交于G点.若
,CE与BF相交于G点.若 =a,
=a, =b,试用a,b表示
=b,试用a,b表示 .
.
解:∵B、G、F三点共线,
∴可设 =x
=x +(1-x)
+(1-x) ,
,
即 =xa+
=xa+ b.
b.
同理可设 =y
=y +(1-y)
+(1-y) ,
,
即 =
=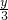 a+(1-y)(a+b)=(1-
a+(1-y)(a+b)=(1- y)a+(1-y)b.
y)a+(1-y)b.
∴xa+ b=(1-
b=(1- y)a+(1-y)b,
y)a+(1-y)b,
∵a、b不共线,
于是得 ,
,
∴解得x= ,
,
∴ =
= a+
a+ b.
b.
分析:根据B、G、F三点共线,得到 =x
=x +(1-x)
+(1-x) ,同理
,同理 =y
=y +(1-y)
+(1-y) ,再利用向量相等的概念,得到关于x,y的方程.即可求解
,再利用向量相等的概念,得到关于x,y的方程.即可求解
点评:本题考查了平面向量的基本定理及其意义,常见结论的利用也对解题由很大帮助,属于基础题.
∴可设
 =x
=x +(1-x)
+(1-x) ,
,即
 =xa+
=xa+ b.
b.同理可设
 =y
=y +(1-y)
+(1-y) ,
,即
 =
=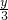 a+(1-y)(a+b)=(1-
a+(1-y)(a+b)=(1- y)a+(1-y)b.
y)a+(1-y)b.∴xa+
 b=(1-
b=(1- y)a+(1-y)b,
y)a+(1-y)b,∵a、b不共线,
于是得
 ,
,∴解得x=
 ,
,∴
 =
= a+
a+ b.
b.分析:根据B、G、F三点共线,得到
 =x
=x +(1-x)
+(1-x) ,同理
,同理 =y
=y +(1-y)
+(1-y) ,再利用向量相等的概念,得到关于x,y的方程.即可求解
,再利用向量相等的概念,得到关于x,y的方程.即可求解点评:本题考查了平面向量的基本定理及其意义,常见结论的利用也对解题由很大帮助,属于基础题.

练习册系列答案
相关题目
 如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).
如图,在平行四边形ABCD中,边AB所在直线方程为2x-y-3=0,点C(3,0).