题目内容
设函数
，
，若实数
、
满足
，
，则（ ）
A． | B． | C． | D． |
D
解析试题分析：由于函数
在
上单调递增，且
，
，且，由零点的存在定理知，
，同理可知
，由于函数
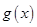在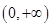
上单调递增，则
，
，于是有，故选D.
考点：1.零点存在定理；2.比较大小
练习册系列答案
相关题目
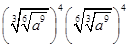等于（ ）
A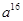． | B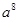． | C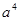． | D． |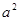
若
，当
时，
的大小关系为（ ）
A． | B． | C． | D． |
下列大小关系正确的是 （ ）
A． | B． |
C． | D． |
函数
的定义域为Ｒ，则实数ｍ的取值范围是（ ）
A． | B． | C． | D． |
设
，则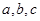
的大小关系为（ ）
A． | B． | C． | D． |
函数
的零点个数是（ ）
| A．2个 | B． 1 个 | C．4个 | D．3个 |
，高为
和
的两矩形所构成．设函数
是图中阴影部分介于平行线
及
之间的那一部分的面积，则函数
的图象大致为( )
下列函数与
有相同图象的一个函数是（ ）
A． | B． |
C． | D． |