题目内容
若直线kx-y+1=0与圆x2+y2+2x-my+1=0交于M,N两点,且M,N关于直线y=-x对称,则|MN|=
.
| 2 |
| 2 |
分析:直线kx-y+1=0与圆x2+y2+2x-my+1=0交于M、N两点,且M、N关于直线y=-x对称,直线y=-x过圆心,即可求出m;然后求出k,通过圆心到直线的距离,半径与半弦长的关系,可以求解|MN|.
解答:解:由题意可知,直线y=-x过圆心,且与直线kx-y+1=0垂直,
∴k=1,
圆x2+y2+2x-my+1=0的圆心坐标(-1,
)在直线x+y=0上,所以m=2,圆心坐标(-1,1),
x2+y2+2x-2y+1=0的半径为1,圆心到直线y=x+1的距离为
=
,
因而弦长是
.
故答案为:
.
∴k=1,
圆x2+y2+2x-my+1=0的圆心坐标(-1,
| m |
| 2 |
x2+y2+2x-2y+1=0的半径为1,圆心到直线y=x+1的距离为
| |-1-1+1| | ||
|
| ||
| 2 |
因而弦长是
| 2 |
故答案为:
| 2 |
点评:本题考查对称知识,圆的一般方程,弦长的求法等知识;是中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ;
;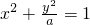 恒有公共点,则a的取值范围为a>1;
恒有公共点,则a的取值范围为a>1; 与
与 的夹角为锐角,则x的取值范围为
的夹角为锐角,则x的取值范围为 ;
;