题目内容

若函数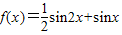

，则对其导函数f'（x）最值的说法正确的是（）
A．只有最小值
B．只有最大值
C．既有最大值又有最小值
D．既无最大值又无最小值

【答案】分析：对f（x）进行求导，得到导数f′（x），再对f′（x）进行求导，利用导数研究导函数的最值问题，从而求解；
解答：解：函数

，
可得f′（x）=

×cos2x×2+cosx=cos2x+cosx=2cos²x-1+cosx=2（cosx+

）²-

，
求f′（x）的最值问题，
∵-1≤cosx≤1，可得，
f（x）有最大值和最小值，
故选C；
点评：此题主要考查导数的运算，以及利用导数研究函数的最值问题，是一道基础题；

练习册系列答案

中考解读考点精练系列答案

中考金牌3年中考3年模拟系列答案

中考精典系列答案

中考模拟卷江苏凤凰教育出版社系列答案

中考模拟试题汇编系列答案

中考内参系列答案

各地期末复习特训卷系列答案

全程金卷冲刺100分系列答案

快乐2加1同步练习系列答案

小博士期末闯关100分系列答案

相关题目

设f（x）是定义在区间（1，+∞）上的函数，其导函数为f′（x）．如果存在实数a和函数h（x），其中h（x）对任意的x∈（1，+∞）都有h（x）＞0，使得f′（x）=h（x）（x²-ax+1），则称函数f（x）具有性质P（a），设函数f（x）=lnx+

(x＞1)，其中b为实数．
（1）①求证：函数f（x）具有性质P（b）；
②求函数f（x）的单调区间．
（2）已知函数g（x）具有性质P（2），给定x₁，x₂∈（1，+∞），x₁＜x₂，设m为实数，α=mx₁+（1-m）x₂，β=（1-m）x₁+mx₂，α＞1，β＞1，若|g（α）-g（β）|＜|g（x₁）-g（x₂）|，求m的取值范围．

（2013•泉州模拟）定义域为D的函数f（x），其导函数为f′（x）．若对?x∈D，均有f（x）＜f′（x），则称函数f（x）为D上的梦想函数．
（Ⅰ）已知函数f（x）=sinx，试判断f（x）是否为其定义域上的梦想函数，并说明理由；
（Ⅱ）已知函数g（x）=ax+a-1（a∈R，x∈（0，π））为其定义域上的梦想函数，求a的取值范围；
（Ⅲ）已知函数h（x）=sinx+ax+a-1（a∈R，x∈[0，π]）为其定义域上的梦想函数，求a的最大整数值．

若函数，则对其导函数值的说法正确的是（　）

Ａ．只有最小值Ｂ．只有最大值

Ｃ．既有最大值又有最小值Ｄ．既无最大值又无最小值

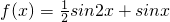若函数 $数学公式$ ，则对其导函数f'（x）最值的说法正确的是

A.
只有最小值
B.
只有最大值
C.
既有最大值又有最小值
D.
既无最大值又无最小值