题目内容
设椭圆
=1(a＞b＞0)的左顶点为A,若椭圆上存在一点P,使∠OPA=
(O为原点),求椭圆离心率的取值范围.
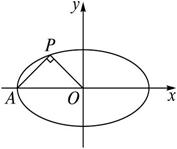
解：如图,设P(x,y),由∠OPA=知点P在以AO为直径的圆上,
即(x+
)2+y2=
.
联立方程组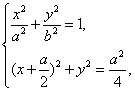
消去y,得
(a2-b2)x2+a3x+a2b2=0.
解得x=-a,或x=
.
当x=-a时,P与A重合,不满足题意,舍去.故P点的横坐标为x=
.
又∵
＞-a,
∴a2＞2b2,
即a2＞2(a2-c2),
即e2=
＞
,e＞
.
又∵0＜e＜1,∴
＜e＜1,
即椭圆离心率的范围是(
,1).
练习册系列答案
轻松夺冠全能掌控卷系列答案
相关题目
=1(a＞b＞0)的右焦点为F1，右准线为l1,若过点F1且垂直于x轴的弦长等于点F1到准线l1的距离，则椭圆的离心率是_________.
=1(a＞b＞0)的面积为πab,过坐标原点的直线l、x轴的正半轴及椭圆围成的两个区域的面积分别为s、t(如图),则s关于t的函数图象的大致形状为
+
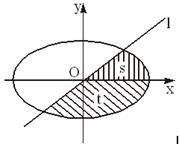
=1(a＞b＞0)的左焦点为F1(－2,0),左准线l1与x轴交于点N(－3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.