题目内容
若函数y=f(x)图象上的任意一点p的坐标(x,y)满足条件|x|≥|y|,则称函数具有性质S,那么下列函数中具有性质S的是( )
| A.f(x)=tanx | B. -1 -1 |
| C.f(x)=sinx | D.f(x)= ln(x+1) |
C
解析试题分析:不等式 表示的平面区域如图所示,函数
表示的平面区域如图所示,函数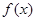 具有性质
具有性质 ,则函数图像必须完全分布在阴影区域①和②部分,
,则函数图像必须完全分布在阴影区域①和②部分, 分布在区域①和③内,
分布在区域①和③内, 分布在区域②和④内,
分布在区域②和④内, 图像分布在区域①和②内,
图像分布在区域①和②内, 在每个区域都有图像,故选
在每个区域都有图像,故选

考点:指数、对数、三角函数的性质和图像、可行域.

练习册系列答案
相关题目
已知函数 ,则
,则 ( )
( )
A. | B. | C.2 | D. |
设函数 的导函数为
的导函数为 ,对任意
,对任意 都有
都有 成立,则( )
成立,则( )
A. | B. |
C. | D. 与 与 的大小不确定 的大小不确定 |
若x0是方程 的解,则x0属于区间( )
的解,则x0属于区间( )
A.( ,1) ,1) | B.( , , ) ) |
C.( , , ) ) | D.(0, ) ) |
若函数 是函数
是函数 的反函数,其图象经过点
的反函数,其图象经过点 ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
设max{f(x),g(x)}= ,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点(
,若函数n(x)=x2+px+q(p,q∈R)的图象经过不同的两点( ,0)、(
,0)、( ,0),且存在整数n使得n<
,0),且存在整数n使得n< <
< <n+1成立,则( )
<n+1成立,则( )
| A.max{n(n),n(n+1)}>1 | B.max{n(n),n(n+1)}<1 |
C.max{n(n),n(n+1)}>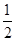 | D.max{n(n),n(n+1)}> 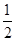 |
 ,
, ,
, ,则( ).
,则( ).



 在
在 上的图象是( )
上的图象是( )