题目内容
已知函数 .
.
(1)解关于x的不等式f(x)>0;
(2)若f(x)+2x≥0在(0,+∞)上恒成立,求实数a的取值范围.
解:(1)不等式f(x)>0,即 >0
>0
整理,得 >0,等价于ax(x-2a)<0
>0,等价于ax(x-2a)<0
因为a≠0,可得
①a>0时,解之得0<x<2a;②a<0时,等价于x(x-2a)>0,解之得x<2a或x>0
综上所述,得:
当a>0时,原不等式的解集为(0,2a);a<0时,原不等式的解集为(-∞,2a)∪(0,+∞).
(2)f(x)+2x≥0在(0,+∞)上恒成立,即
 在(0,+∞)上恒成立,整理得:
在(0,+∞)上恒成立,整理得:
根据基本不等式,得 =4
=4
∴不等式 (0,+∞)上恒成立,即4
(0,+∞)上恒成立,即4 ,解之得a<0或a
,解之得a<0或a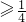 .
.
综上所述,得a的取值范围为(-∞,0)∪[ ,+∞)
,+∞)
分析:(1)由函数的表达式,根据分式不等式的解法将f(x)>0变形整理,再分类讨论并结合一元二次不等式解集的公式,即可得到原不等式的解集.
(2)不等式f(x)+2x≥0在(0,+∞)上恒成立,化简整理可得 在(0,+∞)上恒成立,根据基本不等式求出左边的最小值为4,由此即可得到实数a的取值范围.
在(0,+∞)上恒成立,根据基本不等式求出左边的最小值为4,由此即可得到实数a的取值范围.
点评:本题给出含有参数的函数,讨论不等式恒成立并求不等式的解集,着重考查了函数恒成立的问题、基本不等式求最值和一元二次不等式的解集等知识,属于基础题.
 >0
>0整理,得
 >0,等价于ax(x-2a)<0
>0,等价于ax(x-2a)<0因为a≠0,可得
①a>0时,解之得0<x<2a;②a<0时,等价于x(x-2a)>0,解之得x<2a或x>0
综上所述,得:
当a>0时,原不等式的解集为(0,2a);a<0时,原不等式的解集为(-∞,2a)∪(0,+∞).
(2)f(x)+2x≥0在(0,+∞)上恒成立,即
 在(0,+∞)上恒成立,整理得:
在(0,+∞)上恒成立,整理得:
根据基本不等式,得
 =4
=4∴不等式
 (0,+∞)上恒成立,即4
(0,+∞)上恒成立,即4 ,解之得a<0或a
,解之得a<0或a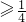 .
.综上所述,得a的取值范围为(-∞,0)∪[
 ,+∞)
,+∞)分析:(1)由函数的表达式,根据分式不等式的解法将f(x)>0变形整理,再分类讨论并结合一元二次不等式解集的公式,即可得到原不等式的解集.
(2)不等式f(x)+2x≥0在(0,+∞)上恒成立,化简整理可得
 在(0,+∞)上恒成立,根据基本不等式求出左边的最小值为4,由此即可得到实数a的取值范围.
在(0,+∞)上恒成立,根据基本不等式求出左边的最小值为4,由此即可得到实数a的取值范围.点评:本题给出含有参数的函数,讨论不等式恒成立并求不等式的解集,着重考查了函数恒成立的问题、基本不等式求最值和一元二次不等式的解集等知识,属于基础题.

练习册系列答案
相关题目
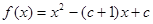
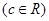 .
.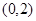 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;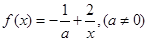 ,
,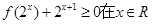 上恒成立,求a的取值范围。
上恒成立,求a的取值范围。 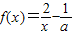 .
.