题目内容
定义:区间[m,n]、(m,n]、[m,n)、(m,n)(n>m)的区间长度为n-m;若某个不等式的解集由若干个无交集的区间的并表示,则各区间的长度之和称为解集的总长度.已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-3,3],则不等式f(x)•g(x)<0解集的总长度的取值范围是
[0,3]
[0,3]
.分析:根据函数的奇偶性关系先判断出f(x)•g(x)<0解集的总长度至多为3,再举出具体例子,得到f(x)•g(x)<0解集的总长度最小是0,即得到答案.
解答:解:∵y=f(x)是偶函数,y=g(x)是奇函数,
∴若x0∈D,使得f(x0)•g(x0)<0,
则f(-x0)•g(-x0)=-f(x0)•g(x0)>0,
∴f(x)•g(x)<0解集的总长度至多为
=3,
例如f(x)=x2,g(x)=x.
如果函数f(x)•g(x)=0的解集总长度不为0,
则f(x)•g(x)<0解集的总长度相应减少,直至为0.
∴解集的总长度的取值范围是[0,3].
故答案为:[0,3].
∴若x0∈D,使得f(x0)•g(x0)<0,
则f(-x0)•g(-x0)=-f(x0)•g(x0)>0,
∴f(x)•g(x)<0解集的总长度至多为
| 3-(-3) |
| 2 |
例如f(x)=x2,g(x)=x.
如果函数f(x)•g(x)=0的解集总长度不为0,
则f(x)•g(x)<0解集的总长度相应减少,直至为0.
∴解集的总长度的取值范围是[0,3].
故答案为:[0,3].
点评:本题以新定义为载体,考查了函数的奇偶性的应用,关键是充分理解新定义的本质,再结合具体的例子进行理解,属于中档题.

练习册系列答案
相关题目
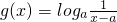 (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].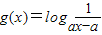 (a>0,a≠1),给定区间[a+2,a+3].
(a>0,a≠1),给定区间[a+2,a+3].