题目内容
求下列函数的定义域与值域:?(1) ![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4) ![]() .
.
解:(1)因为指数函数y=2 x的定义域为x∈R时,值域为y∈(0,+∞);若x≠0,则y≠1;由于![]() 中的
中的![]() ≠0,所以y≠2 0=1.所以所求函数的定义域是{x|x∈R且x≠3},值域为{y|y>0且y≠1}.
≠0,所以y≠2 0=1.所以所求函数的定义域是{x|x∈R且x≠3},值域为{y|y>0且y≠1}.
(2)因为y=(![]() ) |x|中的|x|≥0,所以x∈R,0<y≤1.所以所求函数的定义域为R,值域为{y|0<y≤1}.
) |x|中的|x|≥0,所以x∈R,0<y≤1.所以所求函数的定义域为R,值域为{y|0<y≤1}.
(3)将已知函数整理成y=4 x+2 x+1+1=(2 x) 2+2(2 x)+1=(2 x+1) 2.由此可知定义域为R,值域为{y| y>1}.
(4)已知函数可化为![]() ,由
,由![]() ≥0,得x>1;又由
≥0,得x>1;又由![]() >0,得
>0,得![]() >1.所以定义域为{x| x>1},值域为{y| y>1}.
>1.所以定义域为{x| x>1},值域为{y| y>1}.

练习册系列答案
相关题目
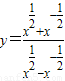 ;
; .
. ;
; .
.