题目内容
(本小题满分12分)
已知二次函数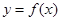 的图象经过原点,且
的图象经过原点,且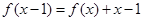 。
。
(1)求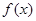 的表达式.
的表达式.
(2)设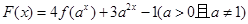 ,当
,当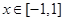 时,
时,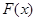 有最大值14,试求
有最大值14,试求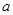 的值.
的值.
【答案】
⑴  (2)
(2) 或
或 .
.
【解析】
试题分析:⑴  函数图象经过原点,
函数图象经过原点,





 5分
5分
(2)、由
得
①当 时
时
令 ,
,




 对称轴
对称轴 ,
,
 在
在 上是增函数。
上是增函数。


 (舍)
(舍)
②当 时
时
令 ,
,




 对称轴
对称轴 ,
,
 在
在 上是增函数。
上是增函数。

 (舍)
(舍)

综上 或
或 .
12分
.
12分
考点:本题主要考查待定系数法,指数函数的性质,二次函数图象和性质。
点评:典型题,利用待定系数法求二次函数解析式,并进一步研究函数的最值,是常见题目。(3)小题中,复合函数问题,利用换元法,转化成二次函数问题,也是常见题目。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目