题目内容
已知函数f(x)=alnx-2x (a为常数).
(1)当a=1时,求函数f(x)的单调区间;
(2)若函数f(x)在区间(1,+∞)上单调递减,求实数a的取值范围;
(3)若函数g(x)=f(x)+x2+1有极值点,求实数a的取值范围.
解:(1)f(x)的定义域为(0,+∞),当a=1时,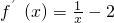
由f′(x)>0得 ,
,
由f′(x)<0,得
∴f(x)的单调增区间为 ,单调减区间为
,单调减区间为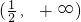 -------(4分)
-------(4分)
(2)f(x)的定义域为(0,+∞)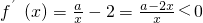 ,即2x-a>0
,即2x-a>0
∵函数在(1,+∞)上为单调减函数,∴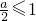 ∴a≤2-----(9分)
∴a≤2-----(9分)
(3)由题意:g(x)=alnx-2x+x2+1∴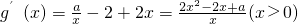 ,
,
若函数g(x)有极值点,∵x>0
∴2x2-2x+a=0有两解且在(0,+∞)至少有一解,----------(11分)
由△=4-8a>0得 ------①----------(13分)
------①----------(13分)
由2x2-2x+a=0在(0,+∞)至少有一解,得a=-2x2+2x在(0,+∞)至少有一解
设y1=a,y2=-2x2+2x(x>0),则有两图象至少有一个交点,
解得 ------②----------(15分)
------②----------(15分)
由①②得 ,
,
综上:当 时函数g(x)有极值点----------(16分)
时函数g(x)有极值点----------(16分)
分析:(1)把a=1代入,先求定义域,在求导数,令f′(x)>0,f′(x)<0,求解函数的单调区间.
(2)先求导数,由函数f(x)在区间(1,+∞)上单调递减,转化成f'(x)≤0在(1,+∞)内恒成立,利用参数分离法即可求出a的范围.
(3)函数g(x)=f(x)+x2+1有极值点,即函数的导数等于0至少一解(且导数在点的两侧符号不相同),求出a的范围即可.
点评:本题考查了函数在某点取得极值的条件、利用导数求函数单调区间,由f′(x)>0(<0)得函数的单调增(减)区间,而在解不等式f′(x)>0(<0)时,如果含有参数时,要注意对参数分类讨论.
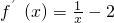
由f′(x)>0得
 ,
,由f′(x)<0,得

∴f(x)的单调增区间为
 ,单调减区间为
,单调减区间为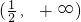 -------(4分)
-------(4分)(2)f(x)的定义域为(0,+∞)
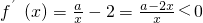 ,即2x-a>0
,即2x-a>0∵函数在(1,+∞)上为单调减函数,∴
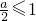 ∴a≤2-----(9分)
∴a≤2-----(9分)(3)由题意:g(x)=alnx-2x+x2+1∴
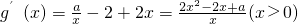 ,
,若函数g(x)有极值点,∵x>0
∴2x2-2x+a=0有两解且在(0,+∞)至少有一解,----------(11分)
由△=4-8a>0得
 ------①----------(13分)
------①----------(13分)由2x2-2x+a=0在(0,+∞)至少有一解,得a=-2x2+2x在(0,+∞)至少有一解
设y1=a,y2=-2x2+2x(x>0),则有两图象至少有一个交点,
解得
 ------②----------(15分)
------②----------(15分)由①②得
 ,
,综上:当
 时函数g(x)有极值点----------(16分)
时函数g(x)有极值点----------(16分)分析:(1)把a=1代入,先求定义域,在求导数,令f′(x)>0,f′(x)<0,求解函数的单调区间.
(2)先求导数,由函数f(x)在区间(1,+∞)上单调递减,转化成f'(x)≤0在(1,+∞)内恒成立,利用参数分离法即可求出a的范围.
(3)函数g(x)=f(x)+x2+1有极值点,即函数的导数等于0至少一解(且导数在点的两侧符号不相同),求出a的范围即可.
点评:本题考查了函数在某点取得极值的条件、利用导数求函数单调区间,由f′(x)>0(<0)得函数的单调增(减)区间,而在解不等式f′(x)>0(<0)时,如果含有参数时,要注意对参数分类讨论.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目