题目内容
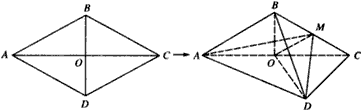
如图，已知菱形ABCD的边长为6，∠BAD=60°，AC∩BD=O。将菱形ABCD沿对角线AC折起，使BD=
3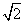
，得到三棱锥B-ACD，
（Ⅰ）若点M是棱BC的中点，求证：OM∥平面ABD；
（Ⅱ）求二面角A-BD-O的余弦值；
（Ⅲ）设点N是线段BD上一个动点，试确定N点的位置，使得CN=4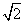，并证明你的结论。
3
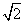，得到三棱锥B-ACD，（Ⅰ）若点M是棱BC的中点，求证：OM∥平面ABD；
（Ⅱ）求二面角A-BD-O的余弦值；
（Ⅲ）设点N是线段BD上一个动点，试确定N点的位置，使得CN=4
，并证明你的结论。 
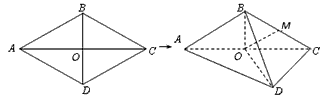
| （Ⅰ）证明：因为点O是菱形ABCD的对角线的交点， 所以O是AC的中点， 又点M是棱BC的中点， 所以OM是△ABC的中位线，OM∥AB， 因为 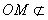 平面ABD， 平面ABD，所以OM∥平面ABD。 |
|
| （Ⅱ）解：由题意，OB=OD=3， 因为 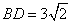 ，所以∠BOD=90°，OB⊥OD，又因为菱形ABCD，所以OB⊥AC，OD⊥AC， 建立空间直角坐标系O-xyz，如图所示，  ，所以  ，设平面ABD的法向量为  （x，y，z），则有  即： ，令x=1，则  ，所以 ，因为AC⊥OB，AC⊥OD，所以AC⊥平面BOD， 平面BOD的法向量与AC平行， 所以平面BOD的法向量为  ， ，因为二面角A-BD-O是锐角， 所以二面角A-BD-O的余弦值为  。 |
 |
（Ⅲ）解：因为N是线段BD上一个动点，设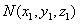 ， ，则  ，所以  ，则  ，由  得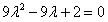 ，即 ，解得  或 ，所以N点的坐标为（0，2，1）或（0，1，2）。 |
练习册系列答案
相关题目
（2012•邯郸一模）如图，已知四棱锥E-ABCD的底面为菱形，且∠ABC=60°，AB=EC=2，AE=BE=
如图，已知在四棱锥P-ABCD中，底面ABCD是菱形，PA⊥底面ABCD，AB=1，PA•AC=1，∠ABC=θ（0＜θ＜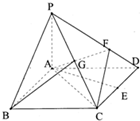
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，点E、G分别是CD、PC的中点，点F在PD上，且PF：FD=2：1．
。 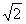