题目内容
已知函数y=2sinx的定义域为[a,b],值域为[-2,1],则b-a的值不可能是
①
;②π;③
;④2π
①③④
①③④
(填序号).①
| π |
| 2 |
| 3π |
| 2 |
分析:由题意,数y=2sinx的定义域为[a,b],值域为[-2,1],则a,b之间的差值必小于一个周期,由此可对函数在此区间上的单调性进行讨论,得出b-a的最大值与最小值,对照所给出的四个数即可得出b-a不可能取到的值.
解答:解:由题意,函数y=2sinx的定义域为[a,b],值域为[-2,1],
∴-1≤sinx≤
若sinx在[a,b]是单调函数,则必有a=2kπ-
,b=2kπ+
,k∈z,此时b-a=
,为最小值
若sinx在[a,b]不是单调函数,则必有a=2kπ-
,b=2kπ+
,k∈z,此时b-a=
,为最大值
考查①
;②π;③
;④2π,只有②π在所求的范围内
故b-a的值不可能是①③④
故答案为①③④
∴-1≤sinx≤
| 1 |
| 2 |
若sinx在[a,b]是单调函数,则必有a=2kπ-
| π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
若sinx在[a,b]不是单调函数,则必有a=2kπ-
| 7π |
| 6 |
| π |
| 6 |
| 4π |
| 3 |
考查①
| π |
| 2 |
| 3π |
| 2 |
故b-a的值不可能是①③④
故答案为①③④
点评:本题考查正弦函数的性质,定义域、值域单调性,解题的关键是根据题设条件找出符合题意的最大区间与最小区间,本题考查了推理判断能力及转化思想,属于中档题,有一定难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
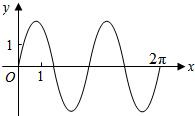 已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=( )
已知函数y=2sin(ωx+φ)(ω>0))在区间[0,2π]的图象如图:那么ω=( )| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin(wx+θ)为偶函数,其图象与直线y=2某两个交点的横坐标分别为x1,x2,若|x2-x1|的最小值为π,则该函数在区间( )上是增函数.
A、(-
| ||||
B、(-
| ||||
C、(0,
| ||||
D、(
|
 下列4个命题:
下列4个命题: