题目内容
设函数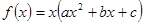 (
(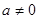 )在
)在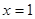 和
和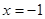 处均有极值,则下列点中一定在
处均有极值,则下列点中一定在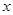 轴上的是( )
轴上的是( )
A.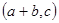 | B.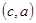 | C.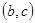 | D.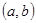 |
D
解析试题分析:即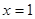 和
和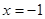 均是方程
均是方程 的根,所以3a+2b+c=0,3a-2b+c=0,解得b=0,所以
的根,所以3a+2b+c=0,3a-2b+c=0,解得b=0,所以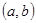 一定在
一定在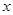 轴上,选D。
轴上,选D。
考点:本题主要考查导数计算,函数极值的概念及求法。
点评:典型题,利用导数求函数的极值,是高考常见题目。求极值的步骤:计算导数、求驻点、讨论驻点附近导数的正负、确定极值。

练习册系列答案
相关题目
已知函数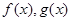 是定义在R上可导函数,满足
是定义在R上可导函数,满足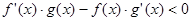 ,且
,且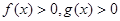 ,对
,对 时。下列式子正确的是( )
时。下列式子正确的是( )
A. | B.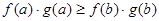 |
C.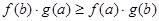 | D.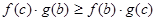 |
设函数 ,
, . 若当
. 若当 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 的取值范围是( ).
的取值范围是( ).
A. | B. | C. | D. |
函数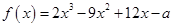 恰有两个不同的零点,则
恰有两个不同的零点,则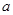 可以是( )
可以是( )
| A.3 | B.4 | C.6 | D.7 |
已知
 ,猜想
,猜想 的表达式为( )
的表达式为( )
A. | B. | C. | D. |
函数y=xlnx在区间 (0,1)上是 ( )
| A.单调增函数 |
| B.单调减函数 |
C.在(0,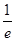 )上是减函数,在( )上是减函数,在(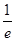 ,1)上是增函数 ,1)上是增函数 |
D.在(0,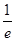 )上是增函数,在( )上是增函数,在(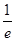 ,1)上是减函数 ,1)上是减函数 |
函数 的单调递增区间( )
的单调递增区间( )
A. | B.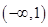 | C. | D. |
给定函数① ②
② ③
③ ④
④ 其中在区间(0,1)上单调递减的函数序号是
其中在区间(0,1)上单调递减的函数序号是
| A.①② | B.②③ | C.③④ | D.①④ |
 的图象为折线
的图象为折线 ,设
,设 ,则函数
,则函数 的图象为( )
的图象为( )



