Question

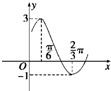已知函数f（x）=Asin（ωx+φ）+b （ω＞0，|φ|＜

π

2

）的图象的一部分如图所示：
（1）求f（x）的表达式；
（2）试写出f（x）的对称轴方程．

Answer 1

分析：（1）根据图象求出函数的振幅A，b，周期T，然后求出ω，将x=

π

6

，y=3代入表达式，求出φ，即可得到函数表达式．
（2）利用正弦函数的对称轴方程，求出函数的对称轴方程即可．

解答：解：（1）由图象可知，函数的最大值M=3，
最小值m=-1，则A=

3-(-1)

2

2，b=

3-1

2

=1，
又T=2(

2

3

π -

π

6

)=π，
∴ω=

2π

T

=

2π

π

=2，
∴f（x）=2sin（2x+φ）+1，
将x=

π

6

，y=3代入上式，得(

π

3

+φ）=1，
∴

π

3

+φ=

π

2

+2kπ，k∈Z，
即φ=

π

6

+2kπ，k∈Z，∴φ=

π

6

，
∴f（x）=2sin(2x+

π

6

)+1．
（2）由2x+

π

6

=

π

2

+kπ，得x=

π

6

+

1

2

kπ，k∈Z，
∴f（x）=2sin(2x+

π

6

)+1的对称轴方程为
x=

π

6

+

1

2

kπ，k∈Z．

点评：本题是基础题，通过函数的图象求出函数解析式，利用基本函数的性质求出函数的对称轴方程，基本知识掌握的好坏，决定解题的好坏，牢记基本函数的性质，是学好数学的关键一环．