题目内容
如图13所示,已知在△A.BC中,D、E、L分别是BC、CA.、A.B的中点,设中线A.D、BE相交于点P.
图13
求证:A.D、BE、CL三线共点.
分析:欲证三条中线共点,只需证明C、P、L三点共线.
证明:设![]() =a.,
=a.,![]() =b,则
=b,则![]() =
=![]() b,
b,![]() =
=![]() -
-![]() =-a+
=-a+![]() b.
b.
设![]() =m
=m![]() ,则
,则![]() +
+![]() =m(
=m(![]() +
+![]() ),
),
![]() =(-1+m)
=(-1+m)![]() +m
+m![]() =(-1+m)a.+m[
=(-1+m)a.+m[![]() (b-a)]=(-1+
(b-a)]=(-1+![]() m)a+
m)a+![]() mb.①
mb.①
又设![]() =n
=n![]() ,则
,则![]() -
-![]() =n(
=n(![]() +
+![]() ),
),
∴![]() =(1-n)
=(1-n)![]() +n
+n![]() =-
=-![]() (1-n)a+n(b-a.)=(-
(1-n)a+n(b-a.)=(-![]() -
-![]() n)a+nb.②
n)a+nb.②
由①②,得 解之,得
解之,得
∴![]() =-
=-![]() a+
a+![]() b=
b=![]() (-a.+
(-a.+![]() b)=
b)=![]()
![]()
∴C、P、L三点共线.∴A.D、BE、CL三线共点.

练习册系列答案
相关题目
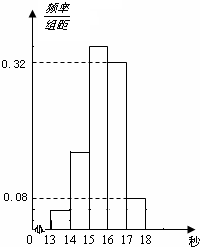 为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8.
为了了解某年段1000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为3:8:19,且第二组的频数为8. 本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分.
本题A、B、C三个选答题,请考生任选一题作答,如果多做,则按所做的第一题计分. (2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为
(2011•滨州一模)我市某商场在春节促销活动中,对2011年2月2日10时至15时的销售额进行统计,其频率分布直方图如图所示,已知10时至11时销售额为3万元,则11时至13时的销售额为