题目内容
已知在平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .(1)求该椭圆的标准方程;
.(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)过原点![]() 的直线交椭圆于点
的直线交椭圆于点![]() ,求
,求![]() 面积的最大值。
面积的最大值。
.(1)由已知得椭圆的半长轴a=2,半焦距c=![]() ,则半短轴b=1.[来源:Z。xx。k.Com]
,则半短轴b=1.[来源:Z。xx。k.Com]
又椭圆的焦点在x轴上, ∴椭圆的标准方程为![]() 4分
4分
(2)设线段PA的中点为M(x,y) ,点P的坐标是(x0,y0),
| 由[来源:学科网ZXXK] |
| 得 | [来源:Z&xx&k.Com]
|
| y= | y0=2y- |
由,点P在椭圆上,得![]() ,
,
∴线段PA中点M的轨迹方程是![]() 8分.
8分.
(3)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入![]() ,
,
解得B(![]() ,
,![]() ),C(-
),C(-![]() ,-
,-![]() ),
),
则 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d=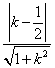 ,
,
∴△ABC的面![]() 积S△ABC=
积S△ABC=![]() 12分
12分
于是S△ABC=![]()
由![]() ≥-1,得S△ABC≤
≥-1,得S△ABC≤![]() ,其中,当k=-
,其中,当k=-![]() 时,等号成立.
时,等号成立.
∴S△ABC的最大值是![]() . 16分
. 16分

练习册系列答案
相关题目