题目内容
已知实数x,y满足 ,每一对整数(x,y)对应平面上一个点,则过这些点中的其中三点可作多少个不同的圆
,每一对整数(x,y)对应平面上一个点,则过这些点中的其中三点可作多少个不同的圆
- A.70
- B.61
- C.52
- D.43
D
分析:画出可行域,找出可行域中的整数点,三点共线的有4种情况,四点共圆的情况(四边形对角互补)有9种,3个正方形,一个矩形,3个等腰梯形,2个满足一组对角为直角的四边形,
由此求得不同的圆的个数是:C93-C53-4C33 -9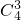 +9,运算求得结果.
+9,运算求得结果.
解答: 解:作出不等式组
解:作出不等式组 可行域
可行域
可行域中所有的整数点有A(-2,0)、B(-1,0)、G(-1,1)、O(0,0)、F(0,1)、H(0,2)、
C(1,0)、E(1,1)、D(2,0),共有9个.
其中,三点共线的有4种情况:AGH,DEH,OFH,EFG.
还有5个点A、B、O、C、D共线.
四点共圆的情况(四边形对角互补)有9种:3个正方形:OCEF,OBGF,OEHG.
一个矩形:CEGB.
五个等腰梯形:ADEG,ACFG,BDEF,DHCF,AHBF.
则可作不同的圆的个数是:C93-C53-4C33 -9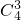 +9=43.
+9=43.
故选 D.
点评:本题主要考查简单的线性规划、排列与组合及两个基本原理,求完成某事件的方法数,常用的方法是排列、组合的方法,有时还用列举的方法,属于中档题.
分析:画出可行域,找出可行域中的整数点,三点共线的有4种情况,四点共圆的情况(四边形对角互补)有9种,3个正方形,一个矩形,3个等腰梯形,2个满足一组对角为直角的四边形,
由此求得不同的圆的个数是:C93-C53-4C33 -9
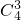 +9,运算求得结果.
+9,运算求得结果.解答:
 解:作出不等式组
解:作出不等式组 可行域
可行域 可行域中所有的整数点有A(-2,0)、B(-1,0)、G(-1,1)、O(0,0)、F(0,1)、H(0,2)、
C(1,0)、E(1,1)、D(2,0),共有9个.
其中,三点共线的有4种情况:AGH,DEH,OFH,EFG.
还有5个点A、B、O、C、D共线.
四点共圆的情况(四边形对角互补)有9种:3个正方形:OCEF,OBGF,OEHG.
一个矩形:CEGB.
五个等腰梯形:ADEG,ACFG,BDEF,DHCF,AHBF.
则可作不同的圆的个数是:C93-C53-4C33 -9
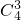 +9=43.
+9=43.故选 D.
点评:本题主要考查简单的线性规划、排列与组合及两个基本原理,求完成某事件的方法数,常用的方法是排列、组合的方法,有时还用列举的方法,属于中档题.

练习册系列答案
相关题目