题目内容
 已知函数y=f(x)的图象如下图所示,则不等式x•f′(x)<0的解集为
已知函数y=f(x)的图象如下图所示,则不等式x•f′(x)<0的解集为
- A.(-∞,
 )∪(
)∪( ,2)
,2) - B.(-∞,
 )∪(2,+∞)
)∪(2,+∞) - C.(-1,0)∪(1,3)
- D.(-∞,0)∪(
 ,2)
,2)
D
分析:由图象先确定原函数的单调性,从而确定导函数在各个范围的正负号,再结合x的正负,即可得不等式的解集
解答:由图象知f(x)在(-∞, )和(2,+∞)上单调递增,在
)和(2,+∞)上单调递增,在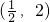 上单调递减
上单调递减
∴f'(x)>0的解集为(-∞, )∪(2,+∞),f'(x)<0的解集为(
)∪(2,+∞),f'(x)<0的解集为( ,2)
,2)
又∵x•f′(x)<0等价于 或
或
∴x<0或 <x<2
<x<2
∴原不等式的解集为(-∞,0)∪( ,2)
,2)
故选D
点评:本题考查原函数的单调性与导函数的正负号的关系.当原函数单调递增时,导函数大于等于0,;当原函数单调递减时,导函数小于等于0.属简单题
分析:由图象先确定原函数的单调性,从而确定导函数在各个范围的正负号,再结合x的正负,即可得不等式的解集
解答:由图象知f(x)在(-∞,
 )和(2,+∞)上单调递增,在
)和(2,+∞)上单调递增,在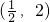 上单调递减
上单调递减∴f'(x)>0的解集为(-∞,
 )∪(2,+∞),f'(x)<0的解集为(
)∪(2,+∞),f'(x)<0的解集为( ,2)
,2)又∵x•f′(x)<0等价于
 或
或
∴x<0或
 <x<2
<x<2∴原不等式的解集为(-∞,0)∪(
 ,2)
,2)故选D
点评:本题考查原函数的单调性与导函数的正负号的关系.当原函数单调递增时,导函数大于等于0,;当原函数单调递减时,导函数小于等于0.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足