题目内容
已知函数f(x)=ax2-|x|+2a-1(a为实常数).
(1)若a=1,求f(x)的单调区间;
(2)若a>0,设f(x)在区间[1,2]的最小值为g(a),求g(a)的表达式.
解:(1)a=1时,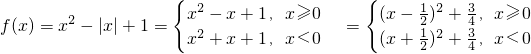 (2分)
(2分)
∴f(x)的单调增区间为( ),(-
),(- ,0)f(x)的单调减区间为(-
,0)f(x)的单调减区间为(-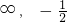 ),(
),( )
)
(2)由于a>0,当x∈[1,2]时,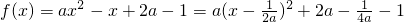
10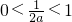 即
即 f(x)在[1,2]为增函数g(a)=f(1)=3a-2
f(x)在[1,2]为增函数g(a)=f(1)=3a-2
20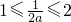 即
即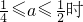 ,
,
30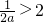 即
即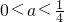 时f(x)在[1,2]上是减函数g(a)=f(2)=6a-3
时f(x)在[1,2]上是减函数g(a)=f(2)=6a-3
综上可得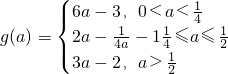 (10分)
(10分)
所以实数a的取值范围是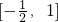
分析:(1)对解析式进行配方整理,根据二次函数顶点点式的形式,结合对称轴来判断函数的单调区间.本题中的函数由于带着绝对值号,故在研究函数性质时要先去绝对值号变成分段函数形式来研究函数的性质.
(2)本小题研究区间区间[1,2]的最小值,故可以直接去掉绝对值号,仍然要配方整理,整理后可以看出,本题是二次函数求最值问题中区间定轴动的问题,故分类讨论对称轴的位置,以确定区间[1,2]单调性,求出最小值为g(a),其形式是一个分段函数的形式.
点评:本题考点是函数的单调性与单调区间,考查的是二次函数的单调性与二次函数在闭区间上的最值问题,二次函数的单调性的研究通常借助其图象来研究,本题中由于函数的系数带着字母,故需要对对称轴的位置进行讨论,用到了分类讨论的思想,区间定轴动是二次函数求最值问题的重要的一类,其规律是在不同的区间段上讨论函数的单调性,做题时要注意总结这一规律.
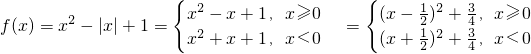 (2分)
(2分)∴f(x)的单调增区间为(
 ),(-
),(- ,0)f(x)的单调减区间为(-
,0)f(x)的单调减区间为(-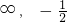 ),(
),( )
)(2)由于a>0,当x∈[1,2]时,
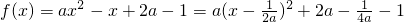
10
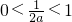 即
即 f(x)在[1,2]为增函数g(a)=f(1)=3a-2
f(x)在[1,2]为增函数g(a)=f(1)=3a-220
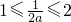 即
即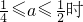 ,
,
30
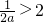 即
即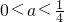 时f(x)在[1,2]上是减函数g(a)=f(2)=6a-3
时f(x)在[1,2]上是减函数g(a)=f(2)=6a-3综上可得
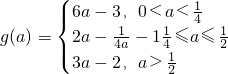 (10分)
(10分)所以实数a的取值范围是
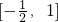
分析:(1)对解析式进行配方整理,根据二次函数顶点点式的形式,结合对称轴来判断函数的单调区间.本题中的函数由于带着绝对值号,故在研究函数性质时要先去绝对值号变成分段函数形式来研究函数的性质.
(2)本小题研究区间区间[1,2]的最小值,故可以直接去掉绝对值号,仍然要配方整理,整理后可以看出,本题是二次函数求最值问题中区间定轴动的问题,故分类讨论对称轴的位置,以确定区间[1,2]单调性,求出最小值为g(a),其形式是一个分段函数的形式.
点评:本题考点是函数的单调性与单调区间,考查的是二次函数的单调性与二次函数在闭区间上的最值问题,二次函数的单调性的研究通常借助其图象来研究,本题中由于函数的系数带着字母,故需要对对称轴的位置进行讨论,用到了分类讨论的思想,区间定轴动是二次函数求最值问题的重要的一类,其规律是在不同的区间段上讨论函数的单调性,做题时要注意总结这一规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目