��Ŀ����
����С������12�֣�ijͬѧ�������о���ѧϰ�У���Դ�����ҹ�²��С��ƶ����ӷ�ѿ����֮��Ĺ�ϵ�����о�����������4�·ݵ�30���������ѡ��5������о����ҷֱ��¼��ÿ����ҹ�²���ÿ��ÿ100�����ӽ��ݺ�ķ�ѿ�����õ��������ϣ�
|
���� |
4��1�� |
4��7�� |
4��15�� |
4��21�� |
4��30�� |
|
�²� |
10 |
11 |
13 |
12 |
8 |
|
��ѿ�� |
23 |
25 |
30 |
26 |
16 |
��1������5������ѡ2�죬�Ƿ�ѿ���������ֱ�Ϊ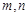 �����¼���
�����¼���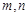 ����С��25���ĸ��ʣ�
����С��25���ĸ��ʣ�
��2������5������ѡ2�죬��ѡȡ����4��1����4��30�յ��������ݣ��������5���е�����������ݣ����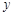 ����
����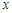 �����Իع鷽��
�����Իع鷽��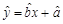 ��
��
��3���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ������ݵ�����������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ����ѡȡ�ļ���������4��1����4��30�յ��������ݣ����ʣ�2�������õ����Իع鷽���Ƿ�ɿ���
���ο���ʽ��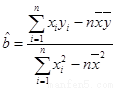
 ��
��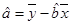 �����ο����ݣ�
�����ο����ݣ�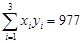 ��
��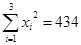 ��
��
��1�� ����2��
����2�� ����3���õ������Իع鷽���ǿɿ���.
����3���õ������Իع鷽���ǿɿ���.
��������(1)�����m,n������ȡֵ���(m,n)��10�֣�Ȼ������� ����С��25�����Ļ����¼���3�����ٸ��ݹŵ�����ʼ��㹫ʽ��ֵ����.
����С��25�����Ļ����¼���3�����ٸ��ݹŵ�����ʼ��㹫ʽ��ֵ����.
��2�����ݹ�ʽ
 ��
�� ,��
,�� .
.
(3)�ڣ�2���Ļ����ϣ��ֱ�x=10��x=8�������Իع鷽�̣������Ӧ��yֵ��Ȼ������ж�Ӧ���ݽ����������Ƿ���2�ţ��������������Ϊ�ɿ���������Ϊ���ɿ�.
�⣺��1�� ������ȡֵ����У�23��25������23��30������23��26������23��16������25��30����25��26������25��16������30��26������30��16������26��16��������10����������2��
������ȡֵ����У�23��25������23��30������23��26������23��16������25��30����25��26������25��16������30��26������30��16������26��16��������10����������2��
�衰 ����С��25��Ϊ�¼�A�����¼�A�����Ļ����¼��У�25��30������25��26����30��26��������
����С��25��Ϊ�¼�A�����¼�A�����Ļ����¼��У�25��30������25��26����30��26�������� �����¼�A�ĸ���Ϊ
�����¼�A�ĸ���Ϊ ��������������6��
��������������6��
��2�������ݵ� ��
�� ��
�� ��
��
�� ��
�� ��
�� 
 ��
�� ��
��
���� ����
���� �����Իع鷽��Ϊ
�����Իع鷽��Ϊ ������������������������10��
������������������������10��
��3���� ʱ��
ʱ�� ��|22-23|
��|22-23| ����
���� ʱ��
ʱ�� |17-16|
|17-16|
���Եõ������Իع鷽���ǿɿ��ģ�����������������������12��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д�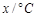
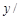 ��
��