题目内容
下列函数中最小正周期是π且图象关于点
成中心对称的一个函数是
- A.y=sin（
- B.y=cos（2x-
- C.y=cos（2x-
- D.y=sin（2x-
C
分析：利用周期公式可排除A，B，再利用“图象关于点成中心对称”即可得答案．
解答：∵y=sin（
+
）的周期T=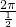
=4π，故可排除A；
同理可排除B；
对于C，∵y=f（x）=cos（2x-），
∴f（
）=cos（2×-）=cos
=0，
∴f（x）=cos（2x-）的图象关于点（，0）成中心对称，故C符合题意；
对于D，y=f（x）=sin（2x-），
f（）=sin（2×-）=sin=1≠0，故D不符，舍去．
故选C．
点评：本题考查三角函数的周期性及其求法，考查余弦函数的对称性，属于中档题．
分析：利用周期公式可排除A，B，再利用“图象关于点
成中心对称”即可得答案．解答：∵y=sin（
+）的周期T=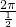=4π，故可排除A；同理可排除B；
对于C，∵y=f（x）=cos（2x-
），∴f（
）=cos（2×-）=cos=0，∴f（x）=cos（2x-
）的图象关于点（，0）成中心对称，故C符合题意；对于D，y=f（x）=sin（2x-
），f（
）=sin（2×-）=sin=1≠0，故D不符，舍去．故选C．
点评：本题考查三角函数的周期性及其求法，考查余弦函数的对称性，属于中档题．
练习册系列答案
相关题目
下列函数中最小正周期是π的函数是（ ）
| A、y=sinx+cosx | B、y=sinx-cosx | C、y=|sinx|+|cosx| | D、t=|sinx+cosx| |