题目内容
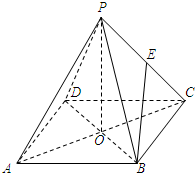
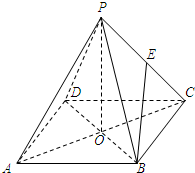 如图,O是正方形ABCD的中心,PO⊥面ABCD,E是PC的中点.PO=
如图,O是正方形ABCD的中心,PO⊥面ABCD,E是PC的中点.PO=| 11 |
| 2 |
(1)求证:BD⊥平面PAC;
(2)求异面直线PA和BE所成的角.
分析:(1)利用线面垂直的性质可得PO⊥BD,结合ABCD是正方形,利用线面垂直的判定可得结论;
(2)连接OE,证明∠OEB是异面直线PA和BE所成的角,在Rt△BOE中,求异面直线PA和BE所成的角.
(2)连接OE,证明∠OEB是异面直线PA和BE所成的角,在Rt△BOE中,求异面直线PA和BE所成的角.
解答:(1)证明:∵PO⊥底面ABCD,BD?面ABCD,∴PO⊥BD…2分
∵ABCD是正方形,∴BD⊥AC…4分
∵PO∩AC=O,PO?平面PAC,AC?平面PAC
∴BD⊥平面PAC…6分
(2)解:连接OE,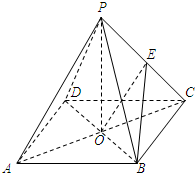
∵O是正方形ABCD的中心,∴OA=OC…7分
在△PAC中,E是PC的中点
∴OE∥PA且OE=
PA…8分
∴∠OEB是异面直线PA和BE所成的角 …9分
在正方形ABCD中,AB=
,∴OB=
BD=1…10分
在Rt△POA中,OA=OB=1,PO=
,∴PA=
=2
…11分
∴OE=
…12分
由(1)知BD⊥平面PAC,且OE?平面PAC,∴BD⊥OE
∴在Rt△BOE中,BE=
=2…13分
∴∠OEB=30°,即异面直线PA和BE所成的角是30°…14分
∵ABCD是正方形,∴BD⊥AC…4分
∵PO∩AC=O,PO?平面PAC,AC?平面PAC
∴BD⊥平面PAC…6分
(2)解:连接OE,

∵O是正方形ABCD的中心,∴OA=OC…7分
在△PAC中,E是PC的中点
∴OE∥PA且OE=
| 1 |
| 2 |
∴∠OEB是异面直线PA和BE所成的角 …9分
在正方形ABCD中,AB=
| 2 |
| 1 |
| 2 |
在Rt△POA中,OA=OB=1,PO=
| 11 |
| OA2+PO2 |
| 3 |
∴OE=
| 3 |
由(1)知BD⊥平面PAC,且OE?平面PAC,∴BD⊥OE
∴在Rt△BOE中,BE=
| OB2+OE2 |
∴∠OEB=30°,即异面直线PA和BE所成的角是30°…14分
点评:本题考查线面垂直,考查异面直线所成的角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
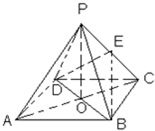 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.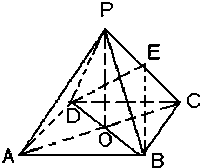 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点. 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: