题目内容
一个盛满水的密闭三棱锥容器S-ABC,不久发现三条侧棱上各有一个小洞D,E,F,且知SD:DA=SE:EB=CF:FS=2:1,若仍用这个容器盛水,则最多可盛原来水的
- A.

- B.

- C.

- D.

D
分析:由实际情况可以得到,当DEF面与清平面平行时,此时盛水最多,由此知,可求出不规则几何体DEFABC的体积,此体积所点三棱锥S-ABC的比即为所求的正确答案.
解答: 解:如右图所示,过DE作与底面ABC平行的截面DEM,
解:如右图所示,过DE作与底面ABC平行的截面DEM,
则M为SC的中点,F为SM的中点.过F作与底面ABC平行的截面FNP,
则N,P分别为SD,SE的中点.
设三棱锥S-ABC的体积为V,高为H,S-DEM的体积为V1,高为h,
则 =
= ,
,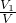 =(
=(  )3=
)3= .
.
三棱锥F-DEM的体积与三棱锥S-DEM的体积的比是1:2,
∴三棱锥F-DEM的体积 .三棱台DEM-ABC的体积=V-V1=
.三棱台DEM-ABC的体积=V-V1= ,
,
∴最多可盛水的容积= +
+ =
= .
.
故最多所盛水的体积是原来的 .
.
故选D.
点评:考查棱柱,棱锥,棱台的体积的求法,解题的关键是掌握分割法求体积是求不规则几何体体积时常用的技巧.
分析:由实际情况可以得到,当DEF面与清平面平行时,此时盛水最多,由此知,可求出不规则几何体DEFABC的体积,此体积所点三棱锥S-ABC的比即为所求的正确答案.
解答:
 解:如右图所示,过DE作与底面ABC平行的截面DEM,
解:如右图所示,过DE作与底面ABC平行的截面DEM,则M为SC的中点,F为SM的中点.过F作与底面ABC平行的截面FNP,
则N,P分别为SD,SE的中点.
设三棱锥S-ABC的体积为V,高为H,S-DEM的体积为V1,高为h,
则
 =
= ,
,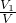 =(
=(  )3=
)3= .
.三棱锥F-DEM的体积与三棱锥S-DEM的体积的比是1:2,
∴三棱锥F-DEM的体积
 .三棱台DEM-ABC的体积=V-V1=
.三棱台DEM-ABC的体积=V-V1= ,
,∴最多可盛水的容积=
 +
+ =
= .
.故最多所盛水的体积是原来的
 .
.故选D.
点评:考查棱柱,棱锥,棱台的体积的求法,解题的关键是掌握分割法求体积是求不规则几何体体积时常用的技巧.

练习册系列答案
相关题目
 B.
B.  C.
C.  D.
D. 